
分析 (1)利用向量共线的性质可得2b=a+c,设a=b-d,c=b+d,由余弦定理解得d=-$\frac{2b}{5}$,进而可得a=$\frac{7b}{5}$,c=$\frac{3b}{5}$,从而可求a:b:c.
(2)由正弦定理可求a,由(1)可求b,c的值,利用三角形面积公式即可计算得解.
解答 解:(1)∵向量$\overrightarrow{m}$与向量$\overrightarrow{n}$共线,可得:$\frac{a-b}{a-c}=\frac{1}{2}$,
∴2b=a+c,
设a=b-d,c=b+d,由已知,cosA=-$\frac{1}{2}$,即$\frac{{b}^{2}+(b+d)^{2}-(b-d)^{2}}{2b(b+d)}$=-$\frac{1}{2}$,
d=-$\frac{2b}{5}$,从而a=$\frac{7b}{5}$,c=$\frac{3b}{5}$,
∴a:b:c=7:5:3.
(2)由正弦定理$\frac{a}{sinA}$=2R,得a=2RsinA=2×14×$\frac{\sqrt{3}}{2}$=14$\sqrt{3}$,
由(1)设a=7k,即k=2$\sqrt{3}$,
所以b=5k=10$\sqrt{3}$,c=3k=6$\sqrt{3}$,
所以S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×10$\sqrt{3}$×6$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=45$\sqrt{3}$,
所以△ABC的面积为45$\sqrt{3}$.
点评 本题主要考查了向量共线的性质,余弦定理,正弦定理,三角形面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | m<1 | B. | m>-1 | C. | -1<m<1 | D. | m>1或m<-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\frac{2\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,3} | C. | {1,5} | D. | {2,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{12}$ | B. | 3 | C. | 2 | D. | $\frac{26}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (${\sqrt{3}$,0) | B. | (${\root{3}{4}$,2] | C. | [${\root{3}{4}$,2) | D. | [${\root{3}{4}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
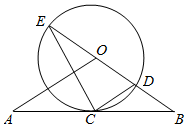 如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC,CD.若tan∠CED=$\frac{1}{2}$,⊙O的半径为3.
如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC,CD.若tan∠CED=$\frac{1}{2}$,⊙O的半径为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com