
���� ��1����an=$\frac{{a}_{n-1}}{��-1��^{n}{a}_{n-1}-2}$��n��2��n��N��������ȡ���������μ���֤����
��2����$sin\frac{��2n-1����}{2}={��-1��^{n-1}}$���ɵ�${b_n}=\frac{{{{��-1��}^{n-1}}}}{{3{{��-2��}^{n-1}}-{{��-1��}^n}}}=\frac{1}{{3•{2^{n-1}}+1}}$��${c_n}=\frac{2}{3}n•��{\frac{1}{b_n}-1}��=n•{2^n}$�������á���λ����������ȱ����е����ʽ���ɵó���
��3��ͨ�������������õȱ����е����ʽ����֤����
��� ��1��֤������an=$\frac{{a}_{n-1}}{��-1��^{n}{a}_{n-1}-2}$��n��2��n��N������
��$\frac{1}{a_n}={��-1��^n}-\frac{2}{{{a_{n-1}}}}$����$\frac{1}{a_n}+{��-1��^n}=��-2��[\frac{1}{{{a_{n-1}}}}+{��-1��^{n-1}}]$��
�֡�$\frac{1}{a_1}+��-1��=3$��������$\left\{{\frac{1}{a_n}+{{��{-1}��}^n}}\right\}$������Ϊ3������Ϊ-2�ĵȱ����У�
��2���⣺��$sin\frac{��2n-1����}{2}={��-1��^{n-1}}$��
��${b_n}=\frac{{{{��-1��}^{n-1}}}}{{3{{��-2��}^{n-1}}-{{��-1��}^n}}}=\frac{1}{{3•{2^{n-1}}+1}}$��
��${c_n}=\frac{2}{3}n•��{\frac{1}{b_n}-1}��=n•{2^n}$
��Sn=1��2+2��22+3��23+��+n��2n����
2Sn=1��22+2��23+3��24+��+��n-1����2n+n��2n+1����
��-�ڣ���-Sn=2+22+23+��+2n-n•2n+1=$\frac{2��1-2n��}{1-2}$-n•2n+1=2n+1-n•2n+1-2��
��Sn=��n-1��2n+1+2��
��3��֤������n��3ʱ����${T_n}=\frac{1}{3+1}+\frac{1}{3•2+1}+\frac{1}{{3•{2^2}+1}}+��+\frac{1}{{3•{2^{n-1}}+1}}$
��$\frac{1}{4}+\frac{1}{7}+\frac{1}{{3•{2^2}}}+\frac{1}{{3•{2^3}}}+\frac{1}{{3•{2^{n-1}}}}=\frac{11}{28}+\frac{{\frac{1}{12}[1-{{��\frac{1}{2}��}^{n-2}}]}}{{1-\frac{1}{2}}}$
=$\frac{11}{28}+\frac{1}{6}[1-{��\frac{1}{2}��^{n-2}}]��\frac{11}{28}+\frac{1}{6}=\frac{47}{84}��\frac{48}{84}=\frac{4}{7}$��
��T1��T2��T3����������n��N*��${T_n}��\frac{4}{7}$��
���� ���⿼���˵��ƹ�ϵ������λ����������ȱ����е�ͨ�ʽ�������ʽ�������������Ǻ�����ֵ�������˷������۷�������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {0��2��4} | B�� | {2��4} | C�� | {0��3��4} | D�� | {3��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ${x^2}-\frac{y^2}{3}=1$ | B�� | ${y^2}-\frac{x^2}{3}=1$ | C�� | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D�� | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [0��1�� | B�� | ��-�ޣ�-3�� | C�� | ∅ | D�� | ��-�ޣ�-3���ȣ�1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
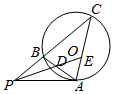 ��ͼ��ֱ��PA�С�O�ڵ�A��ֱ��PB����O�ڵ�B��C����APC�Ľ�ƽ���߷ֱ���AB��AC�ཻ�ڵ�D��E��
��ͼ��ֱ��PA�С�O�ڵ�A��ֱ��PB����O�ڵ�B��C����APC�Ľ�ƽ���߷ֱ���AB��AC�ཻ�ڵ�D��E���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com