
分析 根据圆的半径和余弦定理求出cos∠ACB=$\frac{3}{5}$,根据勾股定理求出CD,∠COD=θ,0≤θ≤π,利用向量的加减的几何意义和向量的数量积的运算,得到$\overrightarrow{OA}$$•\overrightarrow{OB}$=${\overrightarrow{OC}}^{2}$+$\overrightarrow{OC}$•($\overrightarrow{CA}$+$\overrightarrow{CB}$)+$\overrightarrow{CA}•\overrightarrow{CB}$,代值,根据余弦函数的性质计算即可.
解答 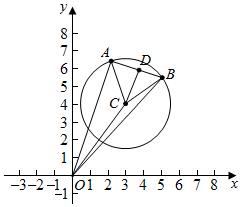 解:∵圆C:(x-3)2+(y-4)2=5,
解:∵圆C:(x-3)2+(y-4)2=5,
∴CA=CB=$\sqrt{5}$,
由余弦定理可得cos∠ACB=$\frac{C{A}^{2}+C{B}^{2}-A{B}^{2}}{2×CA•CB}$=$\frac{5+5-4}{2×5}$=$\frac{3}{5}$,
设D为AB的中点,
∴CD=$\sqrt{A{B}^{2}-A{D}^{2}}$=2,
设∠COD=θ,0≤θ≤π,
∴-1≤cosθ≤1,
∵$\overrightarrow{CA}$+$\overrightarrow{CB}$=2$\overrightarrow{CD}$
∴$\overrightarrow{OA}$$•\overrightarrow{OB}$=($\overrightarrow{OC}$+$\overrightarrow{CA}$)•($\overrightarrow{OC}$+$\overrightarrow{CB}$)=${\overrightarrow{OC}}^{2}$+$\overrightarrow{OC}$•($\overrightarrow{CA}$+$\overrightarrow{CB}$)+$\overrightarrow{CA}•\overrightarrow{CB}$
=5+2$\overrightarrow{OC}$•$\overrightarrow{CD}$+$\sqrt{5}×\sqrt{5}$×$\frac{3}{5}$=8+2×$\sqrt{5}$×2•cosθ=8+4$\sqrt{5}$cosθ,
∴$\overrightarrow{OA}$$•\overrightarrow{OB}$的取值范围为[8-4$\sqrt{5}$,8+4$\sqrt{5}$],
故答案为:[8-4$\sqrt{5}$,8+4$\sqrt{5}$].
点评 本题考查向量的几何意义以及余弦定理,向量的数量积,三角形函数的性质,考查了分析问题,解决问题,运算的能力,以及数形结合和化归思想,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 终边在x轴负半轴上的角是零角 | B. | 第二象限角一定是钝角 | ||
| C. | 第四象限角一定是负角 | D. | 若β=α+k•360°(k∈Z),则α与β终边相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin$\frac{1}{2}$ | B. | cos$\frac{1}{2}$ | C. | 2sin$\frac{1}{2}$-cos$\frac{1}{2}$ | D. | 2cos$\frac{1}{2}$-sin$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com