
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() ,2倍后得到曲线
,2倍后得到曲线![]() ,试写出直线
,试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】下列抽样试验中,适合采用抽签法的是( )
A.从某厂生产的5000件产品中抽取600件进行质量检验
B.从某厂生产的两箱产品(每箱18件)中抽取6件进行质量检验
C.从甲、乙两厂生产的两箱产品(两厂各一箱,每箱18件)中抽取6件进行质量检验
D.从某厂生产的5000件产品中抽取10件进行质量检验
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列表述:①综合法是由因导果法;②综合法是顺推证法;③分析法是执果索因法;④分析法是间接证法;⑤反证法是逆推证法;其中正确的是( )
A.①②③B.③④⑤C.①③④D.②③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,
,
①若f(a)=14,求a的值
②在平面直角坐标系中,作出函数y=f(x)的草图.(需标注函数图象与坐标轴交点处所表示的实数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分为甲、乙两组加工某种零件,在单位时间内每名技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲、乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的技术水平;
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,求该车间“质量合格”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学学生参加数学竞赛培训,在培训期间他们参加5项预赛,成绩如下:
甲:78 76 74 90 82
乙:90 70 75 85 80
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,从平均数、方差的角度考虑,你认为选派哪位学生参加合适?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,其焦点为
,其焦点为![]() .
.
(1)若点![]() ,求以
,求以![]() 为中点的抛物线的弦所在的直线方程;
为中点的抛物线的弦所在的直线方程;
(2)若互相垂直的直线![]() 都经过抛物线
都经过抛物线![]() 的焦点
的焦点![]() ,且与抛物线相交于
,且与抛物线相交于![]() 两点和
两点和![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元。
(1)设铁栅长为![]() 米,一堵砖墙长为
米,一堵砖墙长为![]() 米,求函数
米,求函数![]() 的解析式;
的解析式;
(2)为使仓库总面积![]() 达到最大,正面铁栅应设计为多长?
达到最大,正面铁栅应设计为多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某电子元件进行寿命追踪调查,所得情况如右频率分布直方图.
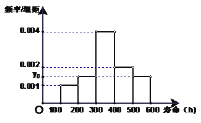
(1)图中纵坐标![]() 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原![]() ;
;
(2)根据图表的数据按分层抽样,抽取![]() 个元件,寿命为
个元件,寿命为![]() 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在![]() 之间的元件中任取
之间的元件中任取![]() 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为![]() ,一个寿命为
,一个寿命为![]() ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com