练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线，其焦点为.

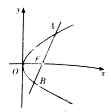
    （1）若点，求以为中点的抛物线的弦所在的直线方程；

    （2）若互相垂直的直线都经过抛物线的焦点，且与抛物线相交于两点和两点，求四边形面积的最小值.

    【答案】（1）；（2）.

    【解析】

    试题分析：（1）用点差法求中点弦所在的直线方程；（2）利用抛物线的定义求抛物线的焦点弦长，表示四边形的面积，再利用均值不等式求面积的最值.

    试题解析：（1）因为点抛物线含焦点的区域内，所以中点弦所在的直线存在.设所求直线交拋物线于,,则,, 所求直线方程为: .

    依题意知，直线的斜率存在，设直线的方程为,与抛物线方程联立，得

    ,消，整理得，其两根为, 且.

    由抛物线的定义可知, , 同理,所以四边形的面积.当且仅当时取得最小值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况，需从这600个销售点中抽取一个容量为100的样本，记这项调查为①；在丙地区有10个特大型销售点，要从中抽取7个销售点调查其销售收入和售后服务等情况，记这项调查为②，则完成①②这两项调查宜采用的抽样方法分别为_____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业接到生产3000台某产品的三种部件的订单，每台产品需要这三种部件的数量分别为2，2，1（单位：件）．已知每个工人每天可生产部件6件，或部件3件，或部件2件．该企业计划安排200名工人分成三组分别生产这三种部件，生产部件的人数与生产部件的人数成正比，比例系数为（为正整数）．

    （1）设生产部件的人数为，分别写出完成三件部件生产需要的时间；

    （2）假设这三种部件的生产同时开工，试确定正整数的值，使完成订单任务的时间最短，并给出时间最短时具体的人数分组方案．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知曲线（为参数），以平面直角坐标系的原点为极点，轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线.

    （1）将曲线上的所有点的横坐标、纵坐标分别伸长为原来的，2倍后得到曲线，试写出直线的直角坐标方程和曲线的参数方程；

    （2）在曲线上求一点，使点到直线的距离最大，并求出此最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 已知函数（，）的图像关于直线x＝对称，最大值为3，且图像上相邻两个最高点的距离为．

    （1）求的最小正周期；

    （2）求函数的解析式；

    （3）若,求．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体为一简单组合体，在底面中，，，，平面，，，．

    （1）求证：平面平面；

    （2）求该组合体的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4—4：坐标系与参数方程。

    在平面直角坐标系xOy中，已知曲线，以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线．

    （1）将曲线上的所有点的横坐标、纵坐标分别伸长为原来的、2倍后得到曲线，试写出直线的直角坐标方程和曲线的参数方程；

    （2）在曲线上求一点P，使点P到直线的距离最大，并求出此最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】抛掷两颗骰子，计算：

    （1）事件“两颗骰子点数相同”的概率；

    （2）事件“点数之和小于7”的概率；

    （3）事件“点数之和等于或大于11”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项为和Sn，点（n，）在直线y＝x＋上．数列{bn}满足bn+2－2bn+1＋bn＝0（nN*），且b3＝11，前9项和为153．

    （1）求数列{an}，{bn}的通项公式；

    （2）求数列的前项和

    （3）设nN*，f（n）＝问是否存在mN*，使得f（m＋15）＝5f（m）成立？若存在，求出m的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案