解:(1)由g(x)=0,解得x=-2或4,
∵|f(x)|≤|g(x)|对x∈R恒成立,
∴必有

,解得
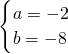
,
此时满足|f(x)|≤|g(x)|.
∴a=-2,b=-8.
(2)由(1)可知:f(x)=x
2-2x-8,
∵对x>2,不等式f(x)≥(m+2)x-m-15恒成立,
∴
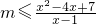
对x>2恒成立.
记u(x)=
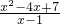
=
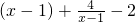
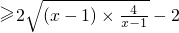
=2,当且仅当x=3时取等号.
∴m≤[u(x)]
min=2.
∴实数m的取值范围是(-∞,2].
(3)∵
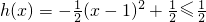
,∴
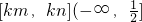
.
∴
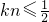
,
又∵
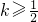
,∴

.
∴[m,n]⊆(-∞,1],
∴h(x)在[m,n]上是增函数.
∴
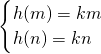
,即
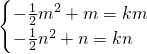
.
解得
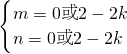
.
又∵
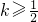
,m<n,
因此:①当

时,[m,n]=[0,2-2k];
②当k>1时,[m,n]=[2-2k,0];
③当k=1时,[m,n]不存在.
分析:(1)由g(x)=0,解得x=-2或4,要使|f(x)|≤|g(x)|对x∈R恒成立,必有

,解出即可;
(2)对x>2,不等式f(x)≥(m+2)x-m-15恒成立?
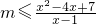
对x>2恒成立,利用基本不等式求得右边的最小值即可.
(3)利用二次函数的单调性,对k分类讨论即可得出.
点评:把恒成立问题正确等价转化,熟练掌握二次函数的单调性、基本不等式的性质、分类讨论的思想方法是解题的关键.

 f(x)-4,那么当k
f(x)-4,那么当k 时,是否存在区间[m,n](m<n),使得函数h(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
时,是否存在区间[m,n](m<n),使得函数h(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由. ,解得
,解得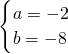 ,
,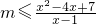 对x>2恒成立.
对x>2恒成立.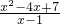 =
=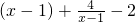
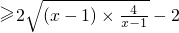 =2,当且仅当x=3时取等号.
=2,当且仅当x=3时取等号.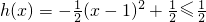 ,∴
,∴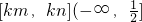 .
.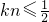 ,
,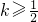 ,∴
,∴ .
.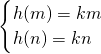 ,即
,即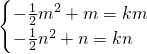 .
.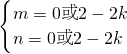 .
.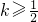 ,m<n,
,m<n, 时,[m,n]=[0,2-2k];
时,[m,n]=[0,2-2k]; ,解出即可;
,解出即可;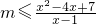 对x>2恒成立,利用基本不等式求得右边的最小值即可.
对x>2恒成立,利用基本不等式求得右边的最小值即可.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<