
【题目】平面上有7个点,每三点的两两连线都组成一个不等边三角形.求证:一定可以找到4对三角形,使每对三角形的公共边既是其中一个三角形的最长边又是另一个三角形的最短边.
【答案】见解析
【解析】
记平面上的7个点为![]() ,
,![]() ,…,
,…,![]() .因为每三点两两连线都组成不等边三角形,故每个三角形都有最长边,也都有最短边.现将每个三角形的最长边都染上红色,剩下的边染上蓝色,则每一个三角形都有红色边.
.因为每三点两两连线都组成不等边三角形,故每个三角形都有最长边,也都有最短边.现将每个三角形的最长边都染上红色,剩下的边染上蓝色,则每一个三角形都有红色边.
下面证明:![]() 个三角形中必有4个同色三角形.
个三角形中必有4个同色三角形.
(1)6阶完全图的边作二染色,至少有2个同色三角形.
设![]() 的引线中有
的引线中有![]() 条红线,
条红线,![]() 条蓝线,以
条蓝线,以![]() 为顶点的非同色三角形有
为顶点的非同色三角形有![]() 个.
个.
由![]() ,知
,知![]() .
.
则非同色三角形总计为![]() .
.
故同色三角形的个数![]() 应满足
应满足![]() .
.
(2)7阶完全图的边作二染色,至少有4个同色三角形.
由(1)的证明知,此时,至少有2个同色三角形.不妨设其中一个为![]() ,去掉
,去掉![]() ,对剩下的6个点又应有2个同色三角形,且异于
,对剩下的6个点又应有2个同色三角形,且异于![]() ,这就得到3个同色三角形.
,这就得到3个同色三角形.
这3个同色三角形有9个顶点,取自7个不同的点,故至少有2个顶点重合于某一![]() ,去掉
,去掉![]() ,则去掉了2个同色三角形,剩下的6个点又应有2个同色三角形,它们与被去掉的2个同色三角形是不相同的,故一共有4个不同的同色三角形.
,则去掉了2个同色三角形,剩下的6个点又应有2个同色三角形,它们与被去掉的2个同色三角形是不相同的,故一共有4个不同的同色三角形.
(3)由于每一个三角形都有红边,这4个同色三角形必为红色三角形,每个红色三角形的最短边必为另一个三角形的最长边.这就找到了4条连线(每个红色三角形的最短边,即使是两个红色三角形的公共边也没有关系),每一条既是一个三角形的最长边(红色),又是另一个三角形(所在红色三角形)的最短边.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示的几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 相交于
相交于![]() 点,四边形
点,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.
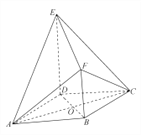
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产基地有五台机器,现有五项工作待完成,每台机器完成每项工作后获得的效益值如表所示.若每台机器只完成一项工作,且完成五项工作后获得的效益值总和最大,则下列叙述错误的的是_____________.
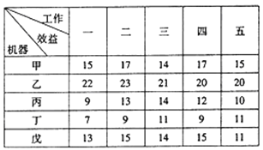
①甲只能承担第四项工作
②乙不能承担第二项工作
③丙可以不承担第三项工作
④丁可以承担第三项工作
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 、
、![]() 为大于3的整数,将
为大于3的整数,将![]() 的立方体分割为
的立方体分割为![]() 个单位正方体,从一角的单位正方体起第
个单位正方体,从一角的单位正方体起第![]() 层、第
层、第![]() 行、第
行、第![]() 列的单位正方体记为
列的单位正方体记为![]() .求所有有序六元数组
.求所有有序六元数组![]() 的个数,使得一只蚂蚁从
的个数,使得一只蚂蚁从![]() 出发,经过每个小正方体恰一次到达
出发,经过每个小正方体恰一次到达![]() .(注)蚂蚁可以从一个单位正方体爬到另一个与之有公共面的相邻正方体.
.(注)蚂蚁可以从一个单位正方体爬到另一个与之有公共面的相邻正方体.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 作直线
作直线![]() 与抛物线交于点
与抛物线交于点![]() 、
、![]() .
.
(1)求证:![]() 不是直角三角形.
不是直角三角形.
(2)当![]() 的斜率为
的斜率为![]() 时,抛物线上是否存在点
时,抛物线上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,求出所有的点
为直角三角形?若存在,求出所有的点![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历戊戌年即将结束,为了迎接新年,小康、小梁、小谭、小刘、小林每人写了一张心愿卡,设计了一个与此心愿卡对应的漂流瓶.现每人随机的选择一个漂流瓶将心愿卡放入,则事件“至少有两张心愿卡放入对应的漂流瓶”的概率为___
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=![]() ,
,
(1)求f(x)的最小值;
(2)对任意![]() ,
,![]() 都有恒成立,求实数a的取值范围;
都有恒成立,求实数a的取值范围;
(3)证明:对一切![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() 与短轴的一个端点构成一个等边三角形,且直线
与短轴的一个端点构成一个等边三角形,且直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com