
【题目】已知![]() 、
、![]() 、
、![]() 为大于3的整数,将
为大于3的整数,将![]() 的立方体分割为
的立方体分割为![]() 个单位正方体,从一角的单位正方体起第
个单位正方体,从一角的单位正方体起第![]() 层、第
层、第![]() 行、第
行、第![]() 列的单位正方体记为
列的单位正方体记为![]() .求所有有序六元数组
.求所有有序六元数组![]() 的个数,使得一只蚂蚁从
的个数,使得一只蚂蚁从![]() 出发,经过每个小正方体恰一次到达
出发,经过每个小正方体恰一次到达![]() .(注)蚂蚁可以从一个单位正方体爬到另一个与之有公共面的相邻正方体.
.(注)蚂蚁可以从一个单位正方体爬到另一个与之有公共面的相邻正方体.
【答案】见解析
【解析】
按照国际象棋棋盘的染色规则交替地将各个单位正方体染为黑色或白色,其中,![]() 为黑色.
为黑色.
当![]() 为偶数时,任两个异色的小正方体满足条件;当
为偶数时,任两个异色的小正方体满足条件;当![]() 为奇数时,任两个黑色的小正方体满足条件.
为奇数时,任两个黑色的小正方体满足条件.
首先证明三个引理.
引理l (i)在![]() 立方体中,异色的两个小正方体满足条件;
立方体中,异色的两个小正方体满足条件;
(ii)在![]() 立方体中,黑色的两个小正方体满足条件.
立方体中,黑色的两个小正方体满足条件.
引理l的证明 由文[1]加试第四题可证.
引理2 在![]() 立方体中,
立方体中,![]()
满足条件,其中,![]() ,即
,即![]() 、
、![]() 异色.
异色.
引理2的证明 在第l层中,由引理l(i),有![]() 满足条件,其路径为
满足条件,其路径为![]()
![]() …
…![]() ,
,
其为黑白相间的.则在![]() 立方体中,对
立方体中,对![]() ,
,![]() ,用
,用
![]()
![]() …
…![]()
![]()
![]() …
…![]()
代替![]()
![]() ,而
,而![]()
![]() 不变.
不变.
【注】为同一层相邻,为不同层相邻.
故在![]() 立方体中,
立方体中,![]() 满足条件.
满足条件.
引理3 在![]() 立方体中,
立方体中,![]()
满足条件,其中,![]() ,即
,即![]() 、
、![]() 异色.
异色.
引理3的证明 在第l层中,由引理l(i),有![]() (与
(与![]() 异色)满足条件,取第2层中与
异色)满足条件,取第2层中与![]() 相邻的小正方体为
相邻的小正方体为![]() ;类似有
;类似有![]()
![]() …
…![]() ,
,
其中,![]() 、
、![]() 分别为第
分别为第![]() 层与
层与![]() 、
、![]() 同色的小正方体
同色的小正方体
故在![]() 正方体中,
正方体中,![]() 满足条件.
满足条件.
回到原题.
(1)![]() 为偶数.
为偶数.
不妨设![]() 为偶数,异色的小正方体
为偶数,异色的小正方体![]() 、
、![]() 分别在第
分别在第![]() 、
、![]() 层(
层(![]() ).
).
若![]() ,则将
,则将![]() 立方体按
立方体按![]() 层、
层、![]() 层、
层、![]() 层分成三部分,在上、下两部分应用引理2,在中间部分应用引理l(i)或引理3,得到在
层分成三部分,在上、下两部分应用引理2,在中间部分应用引理l(i)或引理3,得到在![]() 立方体中的路径
立方体中的路径
![]()
![]()
![]() (
(![]() 、
、![]() 同引理3).
同引理3).
若![]() ,则将
,则将![]() 立方体按
立方体按![]() 层、
层、![]() 层分成两部分,类似得在
层分成两部分,类似得在![]() 立方体中的路径
立方体中的路径
![]()
![]() .
.
若![]() ,则将
,则将![]() 立方体按
立方体按![]() 层、
层、![]() 层、
层、![]() 层分成三部分.
层分成三部分.
在第![]() 层,由引理l(i)有
层,由引理l(i)有![]()
![]() …
…![]() .
.
取![]() ,则由引理2知在上、下两部分中分别有
,则由引理2知在上、下两部分中分别有![]() ,
,![]() 满足条件.
满足条件.
从而,在![]() 立方体中有路径
立方体中有路径
![]() …
…![]()
![]()
![]() …
…![]()
![]()
![]() …
…![]() ,其中,
,其中,![]() 、
、![]() 分别为第
分别为第![]() 层的小正方体
层的小正方体
(2)![]() 为奇数.
为奇数.
若黑色的小正方体![]() 、
、![]() 在
在![]() 立方体的对角,则由引理l(ii),仿引理2可构造
立方体的对角,则由引理l(ii),仿引理2可构造![]() 路径满足条件;否则,
路径满足条件;否则,![]() 方体有一面不含
方体有一面不含![]() 、
、![]() ,且
,且![]() 、
、![]() 到该面的投影不同.不妨设
到该面的投影不同.不妨设![]() 、
、![]() ,其中,
,其中,![]() 、
、![]() ,
,![]() .
.
将![]() 立方体先按第l层、第
立方体先按第l层、第![]() 层分成两部分,再将后者按第
层分成两部分,再将后者按第![]() 行、第
行、第![]() 行分成两部分.
行分成两部分.
因![]() 为偶数,所以,由(1)知在后两部分内分别有
为偶数,所以,由(1)知在后两部分内分别有![]() ,
,![]() 满足条件,其中,
满足条件,其中,![]() 、
、![]() 为第2层中的白色小正方体.
为第2层中的白色小正方体.
在第l层中分别取与![]() 、
、![]() 相邻的黑色小正方体,记为
相邻的黑色小正方体,记为![]() 、
、![]() .由引理1(ii)知
.由引理1(ii)知![]() 满足条件.
满足条件.
则![]() 立方体中有路径
立方体中有路径![]()
![]()
![]() .
.
故当![]() 为奇数时,所求为
为奇数时,所求为![]() ; ’
; ’
当![]() 为偶数时,所求为
为偶数时,所求为![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左焦点为
的左焦点为![]() ,且点
,且点![]() 在C上.
在C上.
![]() 求C的方程;
求C的方程;
![]() 设点P关于x轴的对称点为点
设点P关于x轴的对称点为点![]() 不经过P点且斜率为k的直线l与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,若
不经过P点且斜率为k的直线l与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,若![]() ,求k.
,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (
(![]() 为参数),直线l与曲线C分别交于M,N两点.
为参数),直线l与曲线C分别交于M,N两点.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若点![]() ,求
,求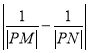 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数,
为参数,![]() ,以
,以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上有7个点,每三点的两两连线都组成一个不等边三角形.求证:一定可以找到4对三角形,使每对三角形的公共边既是其中一个三角形的最长边又是另一个三角形的最短边.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明;
(3)当a>1时,求使f(x)>0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com