
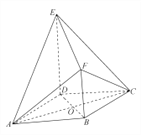
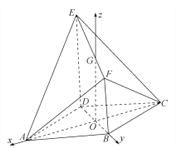
【题目】如图所示的几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 相交于
相交于![]() 点,四边形
点,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)利用题意证得![]() 平面
平面![]() .由面面垂直的判断定理可得平面
.由面面垂直的判断定理可得平面![]() 平面
平面![]() .
.
(2)结合(1)的结论和题意建立空间直角坐标系,由平面的法向量可得二面角![]() 的余弦值为
的余弦值为![]() .
.
试题解析:
(1)因为底面![]() 为菱形,所以
为菱形,所以![]() ,
,
又平面![]() 底面
底面![]() ,平面
,平面![]() 平面
平面![]() ,
,
因此![]() 平面
平面![]() ,从而
,从而![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
由![]() ,
, ![]() ,
, ![]() ,
,
可知![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
从而![]() ,故
,故![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)取![]() 中点
中点![]() ,由题可知
,由题可知![]() ,所以
,所以![]() 平面
平面![]() ,又在菱形
,又在菱形![]() 中,
中, ![]() ,所以分别以
,所以分别以![]() ,
, ![]() ,
, ![]() 的方向为
的方向为![]() ,
, ![]() ,
, ![]() 轴正方向建立空间直角坐标系
轴正方向建立空间直角坐标系![]() (如图示),
(如图示),
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() .
.
由(1)可知![]() 平面
平面![]() ,所以平面
,所以平面![]() 的法向量可取为
的法向量可取为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则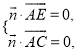 即
即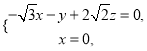 即
即 令
令![]() ,得
,得![]() ,
,
所以![]() .
.
从而![]()
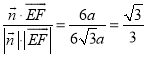 .
.
故所求的二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学中仅有一人申请了北京大学的自主招生考试,当他们被问到谁申请了北京大学的自主招生考试时,甲说:“丙或丁申请了”;乙说:“丙申请了”;丙说:“甲和丁都没有申请”;丁说:“乙申请了”,如果这四位同学中只有两人说的是对的,那么申请了北京大学的自主招生考试的同学是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取100人做调查,得到![]() 列联表,且已知在100个人中随机抽取1人,抽到喜欢游泳的学生的概率为
列联表,且已知在100个人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成![]() 列联表;
列联表;
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
(2)根据列联表,是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由.
附:参考公式与临界值表如下:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
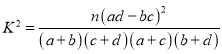
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左焦点为
的左焦点为![]() ,且点
,且点![]() 在C上.
在C上.
![]() 求C的方程;
求C的方程;
![]() 设点P关于x轴的对称点为点
设点P关于x轴的对称点为点![]() 不经过P点且斜率为k的直线l与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,若
不经过P点且斜率为k的直线l与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,若![]() ,求k.
,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ),在以坐标原点为极点,
),在以坐标原点为极点, ![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(1)试将曲线![]() 与
与![]() 化为直角坐标系
化为直角坐标系![]() 中的普通方程,并指出两曲线有公共点时
中的普通方程,并指出两曲线有公共点时![]() 的取值范围;
的取值范围;
(2)当![]() 时,两曲线相交于
时,两曲线相交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (
(![]() 为参数),直线l与曲线C分别交于M,N两点.
为参数),直线l与曲线C分别交于M,N两点.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若点![]() ,求
,求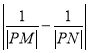 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上有7个点,每三点的两两连线都组成一个不等边三角形.求证:一定可以找到4对三角形,使每对三角形的公共边既是其中一个三角形的最长边又是另一个三角形的最短边.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com