解:(1)∵f′(x)=3x
2-2mx-1,
△=4m
2+12>0,
∴f′(x)=0有两个不相等的实数根:

,
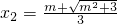
,x
1<x
2.
当x
1<x<x
2时,f′(x)<0,即f(x)单调递减;
当x>x
2或x<x
1时,f′(x)>0,即f(x)单调递增.
综上所述,f(x)的单调递减区间为:[
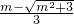
,
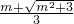
];
单调递增区间为:(-∞,
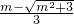
)、(
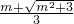
,+∞).
(2)∵对一切的实数x,有f′(x)≥|x|-

成立,
∴3x
2-2mx-1)≥|x|-

,
①当x>0时,
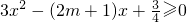
,
即3x+
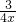
≥2m+1在x>0时恒成立,
因为3x+
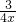
≥2
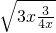
=3,
当x=

时,等号成立,
所以3≥2m+1,即m≤1.
②当x<0时,3|x|
2+(2m-1)|x|+
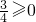
,
即3|x|+
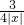
≥1-2m在x<0时,恒成立,
∵3|x|+
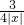

,
当x=-

时等号成立.
所以3≥1-2m,即m≥-1.…(11分)
③当x=0时,m∈R.…(12分)
综上所述,实数m的取值范围是[-1,1].…(13分)
分析:(1)由f′(x)=3x
2-2mx-1,△=4m
2+12>0,知f′(x)=0有两个不相等的实数根:

,
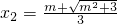
,由此能求出f(x)的单调区间.
(2)由对一切的实数x,有f′(x)≥|x|-

成立,知3x
2-2mx-1)≥|x|-

,由此进行分类讨论,能够求出实数m的取值范围.
点评:本题主要考查函数的性质、导数、不等式等知识,考查数形结合、化归与转化、分类与讨论的数学思想方法,以及运算求解能力,解题时要认真审题,仔细解答,注意合理地进行等价转化.

 成立,其中f′(x)为f(x)的导函数.求实数m的取值范围.
成立,其中f′(x)为f(x)的导函数.求实数m的取值范围. ,
,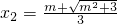 ,x1<x2.
,x1<x2.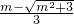 ,
,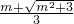 ];
];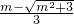 )、(
)、(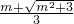 ,+∞).
,+∞). 成立,
成立, ,
,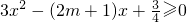 ,
,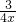 ≥2m+1在x>0时恒成立,
≥2m+1在x>0时恒成立,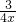 ≥2
≥2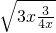 =3,
=3, 时,等号成立,
时,等号成立,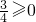 ,
,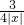 ≥1-2m在x<0时,恒成立,
≥1-2m在x<0时,恒成立,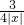
 ,
, 时等号成立.
时等号成立. ,
,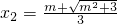 ,由此能求出f(x)的单调区间.
,由此能求出f(x)的单调区间. 成立,知3x2-2mx-1)≥|x|-
成立,知3x2-2mx-1)≥|x|- ,由此进行分类讨论,能够求出实数m的取值范围.
,由此进行分类讨论,能够求出实数m的取值范围.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<