


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
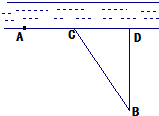 甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,
甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 15 | 16 | 18 | 19 | 22 |
| y | 102 | 98 | 115 | 115 | 120 |
 |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:
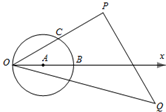 如图,在极坐标系中,设极径为ρ(ρ>0),极角为θ(0≤θ<2π),⊙A的极坐标方程为ρ=2cosθ,点C在极轴的上方,∠AOC=
如图,在极坐标系中,设极径为ρ(ρ>0),极角为θ(0≤θ<2π),⊙A的极坐标方程为ρ=2cosθ,点C在极轴的上方,∠AOC=| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、x+y+2=0 |
| B、x-2y-2=0 |
| C、x-y+4=0 |
| D、2x-y-5=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com