
分析 (Ⅰ)设切点为(x0,y0),根据导数的几何意义即可求出切线方程,
(Ⅱ)构造函数F(x)=f(x)-x-mxf(x)=(1-mx)ln(1+x)-x,求导,再分类讨论,根据导数和函数的最值得关系即可求出.
解答 解:(Ⅰ)由题意可得,f′(x)=$\frac{1}{1+x}$,设切点为(x0,y0),
则切线方程为y-y0=$\frac{1}{{x}_{0}+1}$(x-x0),
∵切线过点(-1,0),
∴0-y0=$\frac{1}{{x}_{0}+1}$(-1-x0),
即-ln(1+x0)=-$\frac{1}{{x}_{0}+1}$(1+x0),解得x0=e-1,
∴y0=1,f′(x0)=$\frac{1}{e}$,
∴切线方程为y-1=$\frac{1}{e}$(x-e+1),即x-ey+1=0,
(Ⅱ)令F(x)=f(x)-x-mxf(x)=(1-mx)ln(1+x)-x,
则F′(x)=-mln(1+x)+$\frac{1-mx}{1+x}$-1,x∈(0,1),
令g(x)=-mln(1+x)+$\frac{1-mx}{1+x}$-1,
g′(x)=-$\frac{mx+2m+1}{(1+x)^{2}}$,
当m≤-$\frac{1}{2}$时,
∵x∈(0,1),
∴g′(x)>0,
则函数F′(x)在(0,1)上单调递增,
∴F′(x)>F′(0)=0,
则函数F(x)在(0,1)单调递增,
∴F(x)>0,
当m≥0时,
∵x∈(0,1),
∴g′(x)<0,
则函数F′(x)在(0,1)上单调递减,
∴F′(x)<F′(0)=0,
则函数F(x)在(0,1)单调递减,
∴F(x)<0,不合题意,
当-$\frac{1}{2}$<m<0时,令x0=min{1,-$\frac{2m+1}{m}$}
当x∈(0,x0]时,g′(x)<0,则函数F′(x)在(0,x0]上单调递减,
∴F′(x)<F′(0)=0,
则函数F(x)在(0,0,x0]单调递减,
∴F(x)<0,不合题意,
综上所述,实数m的取值范围是(-∞,-$\frac{1}{2}$]
点评 本题考查函数的恒成立问题,关键构造函数,利用导数,考查函数的单调性的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
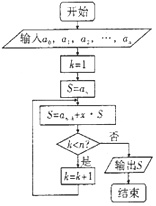 秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )
秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )| A. | 248 | B. | 258 | C. | 268 | D. | 278 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数 | [85,100] | [70,85) | [60,70) | [0,60) |
| 等级 | A等 | B等 | C等 | D等 |
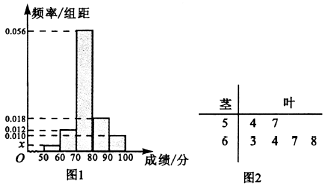
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com