解:(1)f(x)=x(x-a)
2=x
3-2ax
2+a
2x,则f'(x)=3x
2-4ax+a
2=(3x-a)(x-a),
令f'(x)=0,得x=a或

,而g(x)在
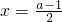
处有极大值,
∴
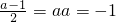
,或
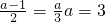
;综上:a=3或a=-1. (4分)
(2)假设存在,即存在
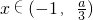
,使得f(x)-g(x)=x(x-a)
2-[-x
2+(a-1)x+a]=x(x-a)
2+(x-a)(x+1)=(x-a)[x
2+(1-a)x+1]>0,
当
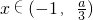
时,又a>0,故x-a<0,
则存在
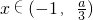
,使得x
2+(1-a)x+1<0,(6分)1°当
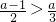
即a>3时,
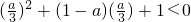
得
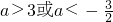
,∴a>3;2°当
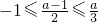
即0<a≤3时,
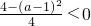
得a<-1或a>3,∴a无解;
综上:a>3. (9分)
(3)据题意有f(x)-1=0有3个不同的实根,g(x)-1=0有2个不同的实根,且这5个实根两两不相等.
(ⅰ)g(x)-1=0有2个不同的实根,只需满足
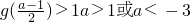
;
(ⅱ)f(x)-1=0有3个不同的实根,1°当
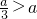
即a<0时,f(x)在x=a处取得极大值,而f(a)=0,不符合题意,舍;2°当
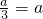
即a=0时,不符合题意,舍;3°当
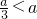
即a>0时,f(x)在
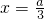
处取得极大值,
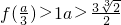
;所以
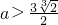
;
因为(ⅰ)(ⅱ)要同时满足,故
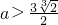
;(注:
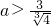
也对)(12分)
下证:这5个实根两两不相等,
即证:不存在x
0使得f(x
0)-1=0和g(x
0)-1=0同时成立;
若存在x
0使得f(x
0)=g(x
0)=1,
由f(x
0)=g(x
0),即x
0(x
0-a)
2=-x
02+(a-1)x
0+a,
得(x
0-a)(x
02-ax
0+x
0+1)=0,
当x
0=a时,f(x
0)=g(x
0)=0,不符合,舍去;
当x
0≠a时,既有x
02-ax
0+x
0+1=0①;
又由g(x
0)=1,即-x
02+(a-1)x
0+a②;
联立①②式,可得a=0;
而当a=0时,H(x)=[f(x)-1]•[g(x)-1]=(x
3-1)(-x
2-x-1)=0没有5个不同的零点,故舍去,所以这5个实根两两不相等.
综上,当
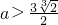
时,函数y=H(x)有5个不同的零点. (16分)
分析:(1)对函数f(x)求导可得f'(x)=3x
2-4ax+a
2=(3x-a)(x-a),由f'(x)=0,可得得x=a或

,而g(x)在
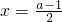
处有极大值,从而可得a
(2)假设存在,即存在
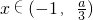
,使得f(x)-g(x)>0,由
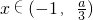
,及a>0,可得x-a<0,
则存在
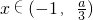
,使得x
2+(1-a)x+1<0,结合二次函数的性质求解
(3)据题意有f(x)-1=0有3个不同的实根,g(x)-1=0有2个不同的实根,且这5个实根两两不相等.g(x)-1=0有2个不同的实根,只需满足
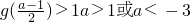
;f(x)-1=0有3个不同的实根,从而结合导数进行求解
点评:本题主要考查了导数在求解极值中的应用,解得本题不但要熟练掌握函数的导数的相关的知识,还要具备一定的逻辑推理的能力,此题对考生的能力要求较高.

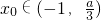 ,使得f(x0)>g(x0),若存在,请求出实数a的取值范围;若不存在,请说明理由.
,使得f(x0)>g(x0),若存在,请求出实数a的取值范围;若不存在,请说明理由. ,而g(x)在
,而g(x)在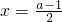 处有极大值,
处有极大值,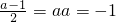 ,或
,或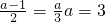 ;综上:a=3或a=-1. (4分)
;综上:a=3或a=-1. (4分)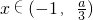 ,使得f(x)-g(x)=x(x-a)2-[-x2+(a-1)x+a]=x(x-a)2+(x-a)(x+1)=(x-a)[x2+(1-a)x+1]>0,
,使得f(x)-g(x)=x(x-a)2-[-x2+(a-1)x+a]=x(x-a)2+(x-a)(x+1)=(x-a)[x2+(1-a)x+1]>0,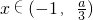 时,又a>0,故x-a<0,
时,又a>0,故x-a<0,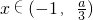 ,使得x2+(1-a)x+1<0,(6分)1°当
,使得x2+(1-a)x+1<0,(6分)1°当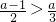 即a>3时,
即a>3时,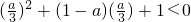 得
得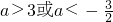 ,∴a>3;2°当
,∴a>3;2°当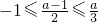 即0<a≤3时,
即0<a≤3时,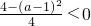 得a<-1或a>3,∴a无解;
得a<-1或a>3,∴a无解;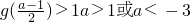 ;
;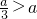 即a<0时,f(x)在x=a处取得极大值,而f(a)=0,不符合题意,舍;2°当
即a<0时,f(x)在x=a处取得极大值,而f(a)=0,不符合题意,舍;2°当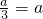 即a=0时,不符合题意,舍;3°当
即a=0时,不符合题意,舍;3°当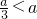 即a>0时,f(x)在
即a>0时,f(x)在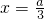 处取得极大值,
处取得极大值,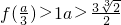 ;所以
;所以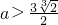 ;
;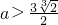 ;(注:
;(注: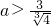 也对)(12分)
也对)(12分)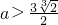 时,函数y=H(x)有5个不同的零点. (16分)
时,函数y=H(x)有5个不同的零点. (16分) ,而g(x)在
,而g(x)在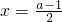 处有极大值,从而可得a
处有极大值,从而可得a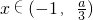 ,使得f(x)-g(x)>0,由
,使得f(x)-g(x)>0,由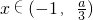 ,及a>0,可得x-a<0,
,及a>0,可得x-a<0,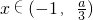 ,使得x2+(1-a)x+1<0,结合二次函数的性质求解
,使得x2+(1-a)x+1<0,结合二次函数的性质求解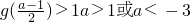 ;f(x)-1=0有3个不同的实根,从而结合导数进行求解
;f(x)-1=0有3个不同的实根,从而结合导数进行求解

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<