考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(Ⅰ)设等差数列的公差为d,并由条件确定d的范围,根据等差数列的通项公式及等比数列的性质、以及题意列出关于首项和公差的方程组,求出公差和首项后代入等差数列的通项公式化简即可;
(Ⅱ)把(Ⅰ)求出的an代入bn,再求出bn+1的表达式,然后作差:bn+1-bn各项相消后再化简,最后把所得的式子与令进行比较,可得bn+1和bn的大小关系.
解答:
解:(Ⅰ)设正项等差数列{a
n}的公差为d,则d≠0,
由a
3+a
10=15,且a
2,a
5,a
11成等比数列得,
| | 2a1+11d=15 ① | | (a1+4d)2=(a1+d)(a1+10d) ② |
| |
,②化为6d
2-3da
1=0,
∵d≠0,∴a
1=2d,代入①解得,
d=1,则a
1=2,
所以,a
n=a
1+(n-1)•d=n+1;
(Ⅱ)由(Ⅰ)和题意得,
bn=++…+,
则
bn+1=++…+,
∴
bn+1-bn=++…+-(++…+)=
+-=
->0,
即b
n+1>b
n.
点评:本题考查了等差数列的通项公式及等比数列的性质,比较大小时常用做差法进行比较,此题的关键是根据条件和公式列出方程组,考查了基础知识和运算能力.



 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案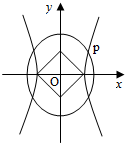 如图,O为坐标原点,双曲线C1:
如图,O为坐标原点,双曲线C1: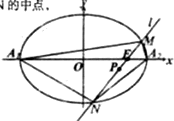 已知椭圆C:
已知椭圆C: