考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由条件可得a
1=1,c
2=1,根据点P(
,1)在上求得
b12=3,可得双曲线C
1的方程.再由椭圆的定义求得a
2=
,可得
b22=
a22-
c22的值,从而求得椭圆C
2的方程.
(Ⅱ)若直线l垂直于x轴,检验部不满足|
+
|≠|
|.若直线l不垂直于x轴,设直线l得方程为 y=kx+m,由
可得y
1•y
2=
.由
可得 (2k
2+3)x
2+4kmx+2m
2-6=0,根据直线l和C
1仅有一个交点,根据判别式△=0,求得2k
2=m
2-3,可得
•≠0,可得|
+
|≠|
|.综合(1)、(2)可得结论.
解答:
解:(Ⅰ)设椭圆C
2的焦距为2c
2,由题意可得2a
1=2,∴a
1=1,c
2=1.
由于点P(
,1)在上,∴
()2-
=1,
b12=3,
∴双曲线C
1的方程为:x
2-
=1.
再由椭圆的定义可得 2a
2=
+
=2
,∴a
2=
,
∴
b22=
a22-
c22=2,∴椭圆C
2的方程为:
+
=1.
(Ⅱ)不存在满足条件的直线l.
(1)若直线l垂直于x轴,则由题意可得直线l得方程为x=
,或 x=-
.
当x=
时,可得 A(
,
)、B(
,-
),求得|
+|=2
,|
|=2
,
显然,|
+
|≠|
|.
同理,当x=-
时,也有|
+
|≠|
|.
(2)若直线l不垂直于x轴,设直线l得方程为 y=kx+m,由
可得
(3-k
2)x
2-2mkx-m
2-3=0,∴x
1+x
2=
,x
1•x
2=
.
于是,y
1•y
2=k
2x
1•x
2+km(x
1+x
2)+m
2=
.
由
可得 (2k
2+3)x
2+4kmx+2m
2-6=0,根据直线l和C
1仅有一个交点,
∴判别式△=16k
2m
2-8(2k
2+3)(m
2-3)=0,∴2k
2=m
2-3.
∴
•=x
1•x
2+y
1•y
2=
≠0,∴
(+)2≠
(-)2,
∴|
+
|≠|
|.
综合(1)、(2)可得,不存在满足条件的直线l.
点评:本题主要考查椭圆的定义、性质、标准方程,直线和圆锥曲线的位置关系的应用,韦达定理,体现了分类讨论的数学思想,属于中档题.

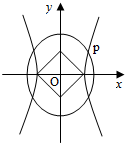 如图,O为坐标原点,双曲线C1:
如图,O为坐标原点,双曲线C1:

 如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上.
如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上. 如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.