
 如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.| BC |
| PH |
| PC |
| AH |
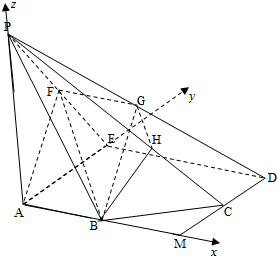 (1)证明:在正方形AMDE中,∵B是AM的中点,
(1)证明:在正方形AMDE中,∵B是AM的中点,| BC |
|
|
| BC |
n•
| ||
|n|•|
|
| 1 |
| 2 |
| π |
| 6 |
| PH |
| PC |
| AH |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
(
|


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
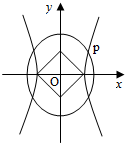 如图,O为坐标原点,双曲线C1:
如图,O为坐标原点,双曲线C1:| x2 | ||
|
| y2 | ||
|
| y2 | ||
|
| x2 | ||
|
2
| ||
| 3 |
| OA |
| OB |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| cosA |
| sinA |
| cosC |
| sinC |
| 1 |
| sinB |
| π |
| 3 |
| ||
| 4 |
| BA |
| BC |
| 3 |
| 2 |
| BC |
| BA |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| sinx |
| x |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com