
 �⣺��1������A�ĺ�����Ϊ3ʱ������A��AG��x����G��
�⣺��1������A�ĺ�����Ϊ3ʱ������A��AG��x����G��| 6p |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| p |
| 4 |
| p |
| 2 |
| p |
| 2 |
| 3 |
| 2 |
| p |
| 4 |
| p |
| 2 |
| P |
| 2 |
| p |
| 2 |
| y1 |
| 2 |
| y1 |
| 2 |
|
| 4 |
| y1 |
| y1 |
| 2 |
| 1 |
| m2 |
| 2 |
| m |
2m+
| ||
m2-
|
| 2m |
| m2-1 |
| 2m |
| m2-1 |
| 2m3 |
| m2-1 |
| 2m |
| m2-1 |
| 2m |
| m2-1 |
| 2m |
| m2-1 |
| y1 |
| 2 |
| ||
| 4 |
| 2 |
| y1 |
| ||
| 4 |
|
| 8 |
| y1 |
| y | 2 1 |
| 8 |
| y1 |
1+
|
1+
|
| 8 |
| y1 |
| 4 | ||
|
| 4 |
| y1 |
|
| ||||||||||||
|
|
| ||||||||
|
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| y1 |
| 4 | ||
|
| ||
| 4 |
| y1 |
| 2 |
| 2 |
| y1 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
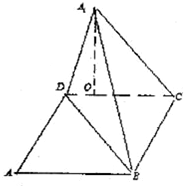 ��ͼ������ABCD�У�AB=10��BC=6���ضԽ���BD�ɡ�ABD����A1BD��λ�ã�ʹA1��ƽ��BCD�ϵ���ӰOǡ����CD�ϣ�
��ͼ������ABCD�У�AB=10��BC=6���ضԽ���BD�ɡ�ABD����A1BD��λ�ã�ʹA1��ƽ��BCD�ϵ���ӰOǡ����CD�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 3 |
| 1 |
| tanA |
| 1 |
| tanC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
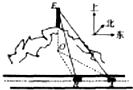 ��ͼ��һ��������һ��ˮƽ�Ĺ�·��������������ʻ����A���ֱ���ɽ��������������E������Ϊ�Ⱥ�ɽ�ŵ�O����O�ǵ�E�ڹ�·����ƽ���ϵ���Ӱ���ķ�λ������ƫ���գ�����ʻakm����B�������ɽ�ŵ�O�ķ�λ������ƫ���£������һ���������ò��������ݺ��йع�ʽд������OE�IJ��裮
��ͼ��һ��������һ��ˮƽ�Ĺ�·��������������ʻ����A���ֱ���ɽ��������������E������Ϊ�Ⱥ�ɽ�ŵ�O����O�ǵ�E�ڹ�·����ƽ���ϵ���Ӱ���ķ�λ������ƫ���գ�����ʻakm����B�������ɽ�ŵ�O�ķ�λ������ƫ���£������һ���������ò��������ݺ��йع�ʽд������OE�IJ��裮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��������AMDE�ı߳�Ϊ2��B��C�ֱ�ΪAM��MD���е㣬������P-ABCDE�У�FΪ��PE���е㣬ƽ��ABF����PD��PC�ֱ��ڵ�G��H��
��ͼ��������AMDE�ı߳�Ϊ2��B��C�ֱ�ΪAM��MD���е㣬������P-ABCDE�У�FΪ��PE���е㣬ƽ��ABF����PD��PC�ֱ��ڵ�G��H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
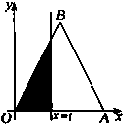 ��ͼ����OAB�DZ߳�Ϊ2���������Σ��ǡ�OABλ��ֱ��x=t��0��t��2������ͼ�ε����Ϊf��t������
��ͼ����OAB�DZ߳�Ϊ2���������Σ��ǡ�OABλ��ֱ��x=t��0��t��2������ͼ�ε����Ϊf��t������2
| ||
| 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com