
【题目】已知函数f(x)=loga ![]() (0<a<1)为奇函数,当x∈(﹣2,2a)时,函数f(x)的值域是(﹣∞,1),则实数a+b= .
(0<a<1)为奇函数,当x∈(﹣2,2a)时,函数f(x)的值域是(﹣∞,1),则实数a+b= .
【答案】![]() +1
+1
【解析】解:∵函数f(x)=loga ![]() (0<a<1)为奇函数,
(0<a<1)为奇函数,
∴f(﹣x)=﹣f(x),
即f(﹣x)+f(x)=0,
∴loga ![]() +loga
+loga ![]() =loga
=loga ![]()
![]() =0,
=0,
即 ![]()
![]() =1,
=1,
∴4﹣x2=b2﹣x2,
即b2=4,解得b=±2,
当b=﹣2时,函数f(x)=loga ![]() =f(x)=loga(﹣1)无意义,舍去.
=f(x)=loga(﹣1)无意义,舍去.
当b=2时,函数f(x)=loga ![]() 为奇函数,满足条件.
为奇函数,满足条件.
∵ ![]() =﹣1+
=﹣1+ ![]() ,在(﹣2,+∞)上单调递减.
,在(﹣2,+∞)上单调递减.
又0<a<1,
∴函数f(x)=loga ![]() 在x∈(﹣2,2a)上单调递增,
在x∈(﹣2,2a)上单调递增,
∵当x∈(﹣2,2a)时,函数f(x)的值域是(﹣∞,1),
∴f(2a)=1,
即f(2a)=loga ![]() =1,
=1,
∴ ![]() =a,
=a,
即1﹣a=a+a2,
∴a2+2a﹣1=0,
解得a=﹣1± ![]() ,
,
∵0<a<1,
∴a= ![]() ﹣1,
﹣1,
∴a+b= ![]() ﹣1+2=
﹣1+2= ![]() +1,
+1,
所以答案是: ![]() +1.
+1.
【考点精析】认真审题,首先需要了解函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇).


科目:高中数学 来源: 题型:
【题目】已知两矩形ABCD与ADEF所在的平面互相垂直,AB=1,若将△DEF沿直线FD翻折,使得点E落在边BC上(即点P),则当AD取最小值时,边AF的长是;此时四面体F﹣ADP的外接球的半径是 . 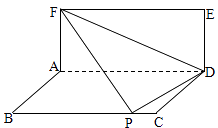
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n∈R,若直线(m+1)x+(n+1)y﹣2=0与圆(x﹣1)2+(y﹣1)2=1相切,则m+n的取值范围是( )
A.[1﹣ ![]() ,1+
,1+ ![]() ]
]
B.(﹣∞,1﹣ ![]() ]∪[1+
]∪[1+ ![]() ,+∞)
,+∞)
C.[2﹣2 ![]() ,2+2
,2+2 ![]() ]
]
D.(﹣∞,2﹣2 ![]() ]∪[2+2
]∪[2+2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x<﹣4,或x>1},B={x|﹣3≤x﹣1≤2}, (Ⅰ)求A∩B、(UA)∪(UB);
(Ⅱ)若{x|2k﹣1≤x≤2k+1}A,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,∠BAD= ![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1﹣BCDE.
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1﹣BCDE. 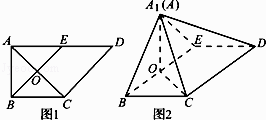
(Ⅰ) 证明:CD⊥平面A1OC;
(Ⅱ) 若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形, 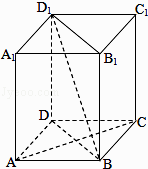
(1)若E为DD1的中点,证明:BD1∥面EAC
(2)求证:AC⊥平面BB1D1D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数 ![]() ,其中x为自变量,a为常数. (I)若当x∈[0,2]时,函数fa(x)的最小值为一1,求a之值;
,其中x为自变量,a为常数. (I)若当x∈[0,2]时,函数fa(x)的最小值为一1,求a之值;
(II)设全集U=R,集A={x|f3(x)≥fa(0)},B={x|fa(x)+fa(2﹣x)=f2(2)},且(UA)∩B≠中,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com