
【题目】定义函数 ![]() ,其中x为自变量,a为常数. (I)若当x∈[0,2]时,函数fa(x)的最小值为一1,求a之值;
,其中x为自变量,a为常数. (I)若当x∈[0,2]时,函数fa(x)的最小值为一1,求a之值;
(II)设全集U=R,集A={x|f3(x)≥fa(0)},B={x|fa(x)+fa(2﹣x)=f2(2)},且(UA)∩B≠中,求a的取值范围.
【答案】解:(Ⅰ)令t=2x,∵x∈[0,2],∴t∈[1,4],
设φ(t)=t2﹣(a+1)t+a,t∈[1,4]
1°当 ![]() ,即a≤1时,fmin(x)=φ(1)=0,与已知矛盾;
,即a≤1时,fmin(x)=φ(1)=0,与已知矛盾;
2°当 ![]() ,即
,即 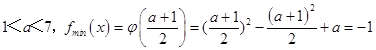 ,
,
解得a=3或a=﹣1,∵1<a<7,∴a=3;
3°当 ![]() ,即a≥7,fmin(x)=φ(4)=16﹣4a﹣4+a=1,
,即a≥7,fmin(x)=φ(4)=16﹣4a﹣4+a=1,
解得 ![]() ,但与a≥7矛盾,故舍去
,但与a≥7矛盾,故舍去
综上所述,a之值为3
(Ⅱ)UA={x|4x﹣42x+3<0}={x|0<x<log23}
B={x|4x﹣(a+1)2x+a+42﹣x﹣(a+1)22﹣x+a=6}= ![]() .
.
由已知(UA)∩B≠即 ![]() ﹣(a+1)(
﹣(a+1)( ![]() )+2a﹣6=0在(0,log23)内有解,
)+2a﹣6=0在(0,log23)内有解,
令t= ![]() ,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,
,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,
也等价于方程 ![]() 在t∈[4,5)上有解
在t∈[4,5)上有解
∵ ![]() 在t∈[4,5)上单调递增,
在t∈[4,5)上单调递增,
∴h(t)∈[﹣1,2)
故所求a的取值范围是[﹣1,2)
【解析】(I)若当x∈[0,2]时,换元,得到φ(t)=t2﹣(a+1)t+a,t∈[1,4],分类讨论,利用函数fa(x)的最小值为﹣1,求a之值;(II)令t= ![]() ,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,也等价于方程
,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,也等价于方程 ![]() 在t∈[4,5)上有解,利用基本不等式,即可求a的取值范围.
在t∈[4,5)上有解,利用基本不等式,即可求a的取值范围.
【考点精析】认真审题,首先需要了解集合的交集运算(交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立),还要掌握函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值)的相关知识才是答题的关键.
B,反之也成立),还要掌握函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知曲线方程C:x2+y2﹣2x﹣4y+m=0.
(1)当m=﹣6时,求圆心和半径;
(2)若曲线C表示的圆与直线l:x+2y﹣4=0相交于M,N,且 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=4,an+1=3an﹣2(n∈N+)
(1)求证:数列{an﹣1}为等比数列,并求出数列{an}的通项公式;
(2)令bn=log3(a1﹣1)+log3(a2﹣1)+…+log3(an﹣1),求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某算法的程序框图如图所示,若将输出(x,y)的值依次记(x1 , y1),(x2 , y2),…(xn , yn), 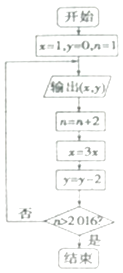
(1)若程序运行中输出的一个数组是(9,t),求t的值;
(2)程序结束时,共输出(x,y)的组数位多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+(b﹣2)x+3(a≠0)
(1)若不等式f(x)>0的解集(﹣1,3).求a,b的值;
(2)若f(1)=2,a>0,b>0求 ![]() +
+ ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值. 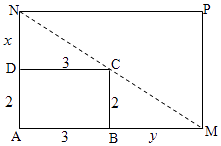
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数p:x2﹣4x﹣12≤0,q:(x﹣m)(x﹣m﹣1)≤0
(1)若m=2,那么p是q的什么条件;
(2)若q是p的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com