
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且直线
,且直线![]() 恰好平分
恰好平分![]() .
.

(1)求![]() 的值;
的值;
(2)设![]() 是直线
是直线![]() 上一点,直线
上一点,直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,定义非零向量
为坐标原点,定义非零向量![]() ,
,![]() 的“相伴函数”为
的“相伴函数”为![]() ,
,
向量![]()
![]() ,
,![]() 称为函数
称为函数![]() 的“相伴向量”.记平面内所有向量的“相伴函数”构成的集合为
的“相伴向量”.记平面内所有向量的“相伴函数”构成的集合为![]() .
.
(1)设函数![]() ,求证:
,求证:![]() ;
;
(2)记![]() ,
,![]() 的“相伴函数”为
的“相伴函数”为![]() ,若函数
,若函数![]() ,
,![]() ,
,![]() 与直线
与直线![]() 有且仅有四个不同的交点,求实数
有且仅有四个不同的交点,求实数![]() 的取值范围;
的取值范围;
(3)已知点![]() ,
,![]() 满足
满足![]() ,向量
,向量![]() 的“相伴函数”
的“相伴函数”![]() 在
在![]() 处取得最大值.当点
处取得最大值.当点![]() 运动时,求
运动时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
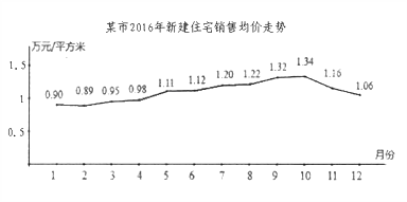
【题目】据某市地产数据研究院的数据显示,2016年该市新建住宅销售均价走势如图所示,为抑制房价过快上涨,政府从8月份采取宏观调控措施,10月份开始房价得到很好的抑制.
参考数据: 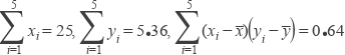 ,(说明:以上数据
,(说明:以上数据 ![]() 为3月至7月的数据)
为3月至7月的数据)
回归方程 ![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: 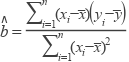 ,
, ![]()
(1)地产数据研究院研究发现,3月至7月的各月均价 ![]() (万元/平方米)与月份
(万元/平方米)与月份 ![]() 之间具有较强的线性相关关系,试建立
之间具有较强的线性相关关系,试建立 ![]() 关于
关于 ![]() 的回归方程(系数精确到 0.01),政府若不调控,依次相关关系预测第12月份该市新建住宅销售均价;
的回归方程(系数精确到 0.01),政府若不调控,依次相关关系预测第12月份该市新建住宅销售均价;
(2)地产数据研究院在2016年的12个月份中,随机抽取三个月份的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,△
为正方形,△![]() 为等边三角形,
为等边三角形,![]() 是
是![]() 中点,平面
中点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(III)记四棱锥![]() 的体积为
的体积为![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,直接写出
,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将甲、乙、丙、丁四个人安排到座位号分别是![]() 的四个座位上,他们分别有以下要求,
的四个座位上,他们分别有以下要求,
甲:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
乙:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
丙:我的要求和乙一样;
丁:如果乙不坐座位号为![]() 的座位,我就不坐座位号为
的座位,我就不坐座位号为![]() 的座位.
的座位.
那么坐在座位号为![]() 的座位上的是( )
的座位上的是( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为了解居民参加体育锻炼的情况,从该社区随机抽取了18名男性居民和12名女性居民,对他们参加体育锻炼的情况进行问卷调查.现按是否参加体育锻炼将居民分成两类:甲类(不参加体育锻炼)、乙类(参加体育锻炼),结果如下表:
甲类 | 乙类 | |
男性居民 | 3 | 15 |
女性居民 | 6 | 6 |
(Ⅰ)根据上表中的统计数据,完成下面的![]() 列联表;
列联表;
男性居民 | 女性居民 | 总计 | |
不参加体育锻炼 | |||
参加体育锻炼 | |||
总计 |
(Ⅱ)通过计算判断是否有90%的把握认为参加体育锻炼与否与性别有关?
附: ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,圆
为坐标原点,圆![]() :
:![]() ,定点
,定点![]() ,点
,点![]() 是圆
是圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 的半径
的半径![]() 于点
于点![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)不垂直于![]() 轴且不过
轴且不过![]() 点的直线
点的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若直线
两点,若直线![]() 、
、![]() 的斜率之和为0,则动直线
的斜率之和为0,则动直线![]() 是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由.
是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰,.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(1)求该选手进入第四轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率;
(3)求该选手回答过四个问题的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com