
| A. | S2016=2016,a1008>a1009 | B. | S2016=-2016,a1008>a1009 | ||
| C. | S2016=2016,a1008<a1009 | D. | S2016=-2016,a1008<a1009 |
分析 (1-a1009)5+2016(1-a1009)=-1,变为:(-1+a1009)5+2016(-1+a1009)=1,令f(x)=x5+2016x-1,f′(x)=5x4+2016>0,因此方程f(x)=0最多有一个实数根.由f(0)<0,f(1)>0,因此f(x)=0有一个实数根x0∈(0,1).再利用等差数列的通项公式、求和公式及其性质即可得出.
解答 解:(1-a1009)5+2016(1-a1009)=-1,变为:(-1+a1009)5+2016(-1+a1009)=1,
令f(x)=x5+2016x-1,f′(x)=5x4+2016>0,因此方程f(x)=0最多有一个实数根.
∵f(0)=-1<0,f(1)=2016>0,
因此f(x)=0有一个实数根x0∈(0,1).
∴1-a1008=a1009-1>0,
可得a1008+a1009=2,a1008<1<a1009.
S2016=$\frac{2016({a}_{1}+{a}_{2016})}{2}$=$\frac{2016({a}_{1008}+{a}_{1009})}{2}$=2016.
故选:C.
点评 本题考查了等差数列的通项公式、求和公式及其性质、利用导数研究函数的单调性、函数的零点,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 | |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
| 模型甲 | 估计值${\hat y_i}^{(1)}$ | 2.4 | 2.1 | 1.6 | ||
| 残差${\hat e_i}^{(1)}$ | 0 | -0.1 | 0.1 | |||
| 模型乙 | 估计值${\hat y_i}^{(2)}$ | 2.3 | 2 | 1.9 | ||
| 残差${\hat e_i}^{(2)}$ | 0.1 | 0 | 0 | |||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
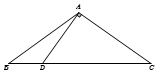 如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | nn | B. | n2 | C. | 2n | D. | n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.
如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计).易拉罐的体积为162πml,设圆柱的高度为hcm,底面半径为rcm,且h≥6r.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为m元/cm2,易拉罐上下底面的制造费用均为n元/cm2(m,n为常数,且0<3m<n).
某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计).易拉罐的体积为162πml,设圆柱的高度为hcm,底面半径为rcm,且h≥6r.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为m元/cm2,易拉罐上下底面的制造费用均为n元/cm2(m,n为常数,且0<3m<n).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com