Question

14．如图，长方体ABCD-A₁B₁C₁D₁中，点M在棱BB₁上，两条直线MA，MC与平面ABCD所成角均为θ，AC与BD交于点O．
（1）求证：AC⊥OM；
（2）当M为BB₁的中点，且θ=$\frac{π}{4}$时，求二面角A-D₁M-B₁的余弦值．

Answer 1

分析 （Ⅰ）由 MC与平面ABCD所成角均为θ，得∠MAB=∠MCB=θ．BA=BC．四边形ABCD为正方形，即可得AC⊥面BDM，即AC⊥OM．
（Ⅱ）  θ=$\frac{π}{4}$时，则有AB=BC=MB，延长D₁M，DB交于点点H，过点O作ON⊥D₁H于点N，连接AN，则∠ANO为二面角A-D₁M-B的平面角，利用平面几何知识即可求解．

解答 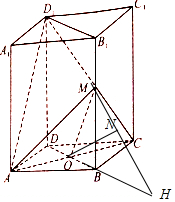解：（Ⅰ）证明：∵MB⊥面ABCD，直线MA，MC与平面ABCD所成角均为θ，∴∠MAB=∠MCB=θ．
故△MBA≌MBC，BA=BC．
∴四边形ABCD为正方形，AC⊥DB，又AC⊥MB，DB∩MB=B
∴AC⊥面BDM，即AC⊥OM．
（Ⅱ）  θ=$\frac{π}{4}$时，则有AB=BC=MB，延长D₁M，DB交于点点H，
过点O作ON⊥D₁H于点N，连接AN，则∠ANO为二面角A-D₁M-B的平面角．
设AB=1，由△D₁DH∽△ONH易得ON=$\frac{\sqrt{6}}{2}$，AO=$\frac{\sqrt{2}}{2}$，
tan∠ANO=$\frac{AO}{ON}=\frac{\sqrt{3}}{3}$，∴∠ANO=30°
二面角A-D₁M-B₁的余弦值为$\frac{\sqrt{3}}{3}$．

点评 本题考查了空间线线垂直的判定，几何法求二面角，考查了转化思想，属于中档题，