
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 晴 | 霾 | 霾 | 阴 | 霾 | 霾 | 阴 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 霾 |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
| 不限行 | 限行 | 总计 | |
| 没有雾霾 | a | ||
| 有雾霾 | b | ||
| 总计 | 30 | 30 | 60 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
分析 (1)根据题意写出a、b的值,计算所求的概率;
(2)设限行时x天没有雾霾,有雾霾为30-x天,利用观测值公式列出不等式,求解即可.
解答 解:(1)根据题意知,a=10,b=30-10=20,
在该年11月份任取一天,估计该市是晴天的概率为P=$\frac{6}{30}$=$\frac{1}{5}$;
(2)设限行时x天没有雾霾,则有雾霾为30-x天,
代入公式${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$≤3,
化简为:21x2-440x+1500≤0,x∈[0,30],且x∈N*,
即(7x-30)(3x-50)≤0,
解得$\frac{30}{7}$≤x≤$\frac{50}{3}$,
所以5≤x≤16,且x∈N*;
所以若没有90%的把握认为雾霾与限行有关系,则限行时有5~16天没有雾霾天气.
点评 本题考查了独立性检验的应用问题,也考查了概率与不等式的计算问题,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
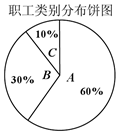 某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 | |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
| 模型甲 | 估计值${\hat y_i}^{(1)}$ | 2.4 | 2.1 | 1.6 | ||
| 残差${\hat e_i}^{(1)}$ | 0 | -0.1 | 0.1 | |||
| 模型乙 | 估计值${\hat y_i}^{(2)}$ | 2.3 | 2 | 1.9 | ||
| 残差${\hat e_i}^{(2)}$ | 0.1 | 0 | 0 | |||
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.
如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com