
分析 z=x2+y2+2(x-y)=(x+1)2+(y-1)2-2利用z的几何意义,利用数形结合即可得到结论.
解答 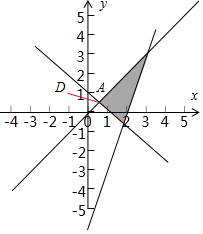 解:作出变量x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≥1\\ y≥3x-6\end{array}\right.$,对应的平面区域如图
解:作出变量x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≥1\\ y≥3x-6\end{array}\right.$,对应的平面区域如图
z=x2+y2+2(x-y)=(x+1)2+(y-1)2-2,则z的几何意义是,区域内的点到点D(-1,1)的距离的平方减2,
$\left\{\begin{array}{l}{y=x}\\{x+y=1}\end{array}\right.$解得A($\frac{1}{2}$,$\frac{1}{2}$)
由图象可知点D到A的距离d即为z=d2-2最小值,
则z=$\frac{1}{4}+\frac{1}{4}+2(\frac{1}{2}-\frac{1}{2})$=$\frac{1}{2}$,
故x2+y2+2(x-y)的最小值为$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查线性规划的应用,利用z的几何意义,结合点到直线的距离公式是解决本题的关键.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 晴 | 霾 | 霾 | 阴 | 霾 | 霾 | 阴 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 霾 |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
| 不限行 | 限行 | 总计 | |
| 没有雾霾 | a | ||
| 有雾霾 | b | ||
| 总计 | 30 | 30 | 60 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14π | B. | 7π | C. | 21π | D. | 28π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com