
分析 (1)求出导函数,对参数m分类讨论,得出函数的极值情况;
(2)g(x)+3f'(x)>0等价于3ex-3x2+6mx-3>0,
构造函数u(x)=3ex-3x2+6mx-3,通过二次求导判断导函数的单调性,进而得出u(x)=3ex-3x2+6mx-3,
得出当x>0时,u(x)>u(0)=0,得出结论成立.
解答 解:(1)f(x)的定义域为(0,+∞),$f'(x)=\frac{2m}{x}-1$=$-\frac{x-2m}{x}$.
①当m≤0时,f'(x)<0,故f(x)在(0,+∞)内单调递减,f(x)无极值;
②当m>0时,令f'(x)>0,得0<x<2m;令f'(x)<0,得x>2m.
故f(x)在x=2m处取得极大值,且极大值为f(2m)=2mln(2m)-2m,f(x)无极小值.
(2)证明:当x>0时,g(x)+3f'(x)>0,
?$\frac{{3{e^x}-3}}{x^2}+\frac{6m}{x}-3>0?$3ex-3x2+6mx-3>0.
设函数u(x)=3ex-3x2+6mx-3,
则u'(x)=3(ex-2x+2m).记v(x)=ex-2x+2m,
则v'(x)=ex-2.
当x变化时,v'(x),v(x)的变化情况如下表:
由上表可知v(x)≥v(ln2),
而v(ln2)=eln2-2ln2+2m=2-2ln2+2m=2(m-ln2+1),
由m>1,知m>ln2-1,
所以v(ln2)>0,
所以v(x)>0,即u'(x)>0.
所以u(x)在(0,+∞)内为单调递增函数.
所以当x>0时,u(x)>u(0)=0.
即当m>1且x>0时,3ex-3x2+6mx-3>0.
所以当m>1且x>0时,总有g(x)+3f'(x)>0.
点评 本题考查了极值的概念和二次求导,利用导数判断函数的单调性,难点是转化思想的应用.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,1) | C. | (-∞,-1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
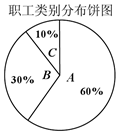 某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com