
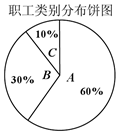
 某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
分析 (Ⅰ)设工种A,B,C职工的每份保单保险公司的效益为随机变量X,Y,Z,
写出随机变量X、Y、Z的分布列,计算保险公司期望收益EX、EY、EZ;
根据要求列出不等式,求出a、b满足的条件;
(Ⅱ)计算企业不与保险公司合作时安全支出(即赔偿金的期望值),
以及企业与保险公司合作的安全支出(即保费),比较大小.
解答 解:(Ⅰ)设工种A,B,C职工的每份保单保险公司的效益为随机变量X,Y,Z,
则随机变量X的分布列为:
| X | a | a-100×104 |
| P | $1-\frac{1}{{{{10}^5}}}$ | $\frac{1}{{{{10}^5}}}$ |
| Y | a | a-100×104 |
| P | $1-\frac{2}{{{{10}^5}}}$ | $\frac{2}{{{{10}^5}}}$ |
| Z | b | b-50×104 |
| P | $1-\frac{1}{{{{10}^4}}}$ | $\frac{1}{{{{10}^4}}}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的计算问题,也考查了不等式的应用问题,是综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{8}})∪[{\frac{1}{8},+∞})$ | B. | $[{-\frac{1}{4},0})∪({0,\frac{1}{8}}]$ | C. | (0,8] | D. | $({-∞,-\frac{1}{4}}]∪[{\frac{1}{8},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 晴 | 霾 | 霾 | 阴 | 霾 | 霾 | 阴 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 霾 |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
| 不限行 | 限行 | 总计 | |
| 没有雾霾 | a | ||
| 有雾霾 | b | ||
| 总计 | 30 | 30 | 60 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com