
分析 (1)根据两角和与差的正弦函数对已知函数关系式进行化简得到f(x)=sin(2x+φ),所以结合正弦函数的性质来求最小正周期和值域;
(2)把( $\frac{π}{6}$,$\frac{1}{2}$)代入函数y=f(x+$\frac{π}{6}$),根据0<φ<π求φ的值.
解答 (1)解:∵f(x)=sin2xcosφ+cos2xsinφ=sin(2x+φ),即f(x)=sin(2x+φ),
∴函数f(x)的最小正周期为π,值域为[-1,1];
(2)解:∵函数y=f(x+$\frac{π}{6}$)=sin(2x+$\frac{π}{3}$+φ),
又点($\frac{π}{6}$,$\frac{1}{2}$)在函数y=f(x+$\frac{π}{6}$)的图象上,
∴sin($\frac{2π}{3}$+φ)=$\frac{1}{2}$.
∵0<φ<π,$\frac{2π}{3}$<$\frac{2π}{3}$+φ<$\frac{5π}{3}$,
∴$\frac{2π}{3}$+φ=$\frac{5π}{6}$,
解得:φ=$\frac{π}{6}$.
点评 本小题主要考查三角函数性质和三角函数的基本关系等知识,考查化归与转化的数学思想方法,以及运算求解能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10个 | B. | 9个 | C. | 8个 | D. | 7个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-1,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 表1 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| P(K2≥k0) | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
| A. | 5% | B. | 2.5% | C. | 1% | D. | 0.5% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
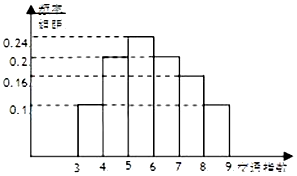 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com