已知函数f(x)=eax-x,其中a≠0.
(1)若对一切x∈R,f(x)≥1恒成立,求a的取值集合.
(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2)(x1<x2),记直线AB的斜率为K,问:是否存在x∈(x1,x2),使f′(x)>k成立?若存在,求x的取值范围;若不存在,请说明理由.
【答案】
分析:(1)先确定a>0,再求导函数,确定函数的单调性,可得
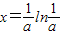
时,f(x)取最小值
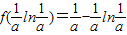
故对一切x∈R,f(x)≥1恒成立,则
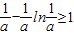
,构建新函数g(t)=t-tlnt,则g′(t)=-lnt,确定函数的单调性,求出函数的最大值,由此即可求得a的取值集合;
(2)由题意知,
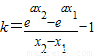
,构建新函数φ(x)=f′(x)-k=
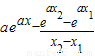
,则
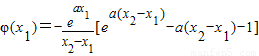
,
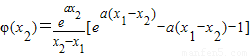
,构建函数F(t)=e
t-t-1,从而可证明φ(x
1)<0,φ(x
2)>0,由此即可得到存在x
∈(x
1,x
2),使f′(x
)>k成立.
解答:解:(1)若a<0,则对一切x>0,函数f(x)=e
ax-x<1,这与题设矛盾,
∵a≠0,∴a>0
∵f′(x)=ae
ax-1,令f′(x)=0,可得
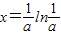
令f′(x)<0,可得
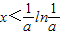
,函数单调减;令f′(x)>0,可得
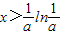
,函数单调增,
∴
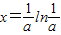
时,f(x)取最小值
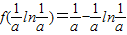
∴对一切x∈R,f(x)≥1恒成立,则
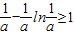
①
令g(t)=t-tlnt,则g′(t)=-lnt
当0<t<1时,g′(t)>0,g(t)单调递增;当t>1时,g′(t)<0,g(t)单调递减
∴t=1时,g(t)取最大值g(1)=1
∴当且仅当
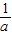
=1,即a=1时,①成立
综上所述,a的取值集合为{1};
(2)由题意知,
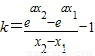
令φ(x)=f′(x)-k=
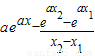
,则

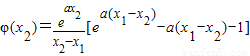
令F(t)=e
t-t-1,则F′(t)=e
t-1
当t<0时,F′(t)<0,函数单调减;当t>0时,F′(t)>0,函数单调增;
∴t≠0时,F(t)>F(0)=0,即e
t-t-1>0
∴
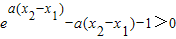
,
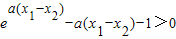
∵
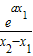
>0,
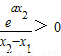
∴φ(x
1)<0,φ(x
2)>0
∴存在c∈(x
1,x
2),φ(c)=0
∵φ′(x)单调递增,故这样的c是唯一的,且
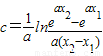
当且仅当x∈(
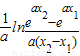
,x
2)时,f′(x)>k
综上所述,存在x
∈(x
1,x
2),使f′(x
)>k成立,且x
的取值范围为(

,x
2)
点评:本题考查导数知识的运用,考查函数的单调性与极值,考查构建新函数确定函数值的符号,从而使问题得解.

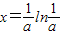 时,f(x)取最小值
时,f(x)取最小值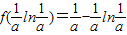
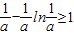 ,构建新函数g(t)=t-tlnt,则g′(t)=-lnt,确定函数的单调性,求出函数的最大值,由此即可求得a的取值集合;
,构建新函数g(t)=t-tlnt,则g′(t)=-lnt,确定函数的单调性,求出函数的最大值,由此即可求得a的取值集合;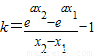 ,构建新函数φ(x)=f′(x)-k=
,构建新函数φ(x)=f′(x)-k=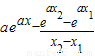 ,则
,则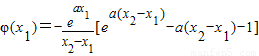 ,
,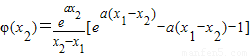 ,构建函数F(t)=et-t-1,从而可证明φ(x1)<0,φ(x2)>0,由此即可得到存在x∈(x1,x2),使f′(x)>k成立.
,构建函数F(t)=et-t-1,从而可证明φ(x1)<0,φ(x2)>0,由此即可得到存在x∈(x1,x2),使f′(x)>k成立.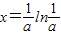
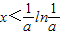 ,函数单调减;令f′(x)>0,可得
,函数单调减;令f′(x)>0,可得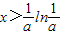 ,函数单调增,
,函数单调增,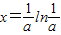 时,f(x)取最小值
时,f(x)取最小值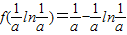
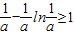 ①
①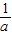 =1,即a=1时,①成立
=1,即a=1时,①成立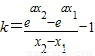
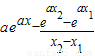 ,则
,则
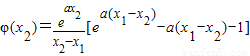
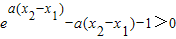 ,
,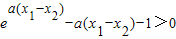
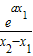 >0,
>0,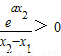
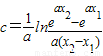
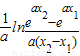 ,x2)时,f′(x)>k
,x2)时,f′(x)>k ,x2)
,x2)
