
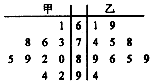
 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.分析 (1)由茎叶图能求出甲学生的平均成绩和方差.
(2)记事件A为“a>b“,由于乙学生的平均成绩为79.6,解得a+b=10,由a,b∈[0,9],且a≥1,b≥1,利用列举法能求出a>b的概率.
解答 解:(1)由茎叶图得甲学生的平均成绩为:
$\overline{x}$=$\frac{1}{10}$(61+73+76+78+80+82+89+85+92+94)=81,
方差为:
S2=$\frac{1}{10}$[(-20)2+(-8)2+(-5)2+(-3)2+(-1)2+12+82+42+112+132]=87.
(2)记事件A为“a>b“,由于乙学生的平均成绩为79.6,
解得a+b=10,
∵a,b∈[0,9],且a≥1,b≥1,
∴a,b的取值为:
(1,9),(2,8),(3,7),(4,6),(5,5),(6,4),(7,3),(8,2),(9,1),
共9种情况,
其中满足a>b的有:(6,4),(7,3),(8,2),(9,1),共4种情况,
∴a>b的概率p=$\frac{4}{9}$.
点评 本题考查概率的求法,涉及到概率、茎叶图、列举法等知识点,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想,是基础题.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
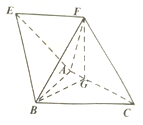 如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.
如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
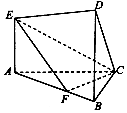 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.
如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com