
分析 利用基本不等式可知an≥a4=$\frac{31}{4}$(n≤5),进而问题转化为当n>5时a≥$\frac{8}{lnn}$恒成立,计算即得结论.
解答 解:由题可知当n≤5时结合函数y=x+$\frac{15}{x}$(x>0),可知an≥a4=4+$\frac{15}{4}$=$\frac{31}{4}$,
又因为{an}的最小值为$\frac{31}{4}$,
所以当n>5时y=alnn-$\frac{1}{4}$≥$\frac{31}{4}$,即alnn≥8,
又因为lnn>ln5>0,
所以当n>5时a≥$\frac{8}{lnn}$恒成立,
所以$a≥\frac{8}{ln6}$,
故答案为:[$\frac{8}{ln6}$,+∞).
点评 本题考查数列的递推式,考查函数的单调性,考查分离参数,考查基本不等式,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $({3,\frac{201}{10}})$ | B. | $({1,\frac{181}{10}})$ | C. | $({2\sqrt{2},+∞})$ | D. | $({2\sqrt{2}-2,+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{15}$ | B. | $\frac{{\sqrt{3}}}{16}$ | C. | $\frac{{\sqrt{2}}}{16}$ | D. | $\frac{{\sqrt{2}}}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
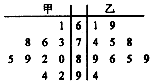 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}+1}{4}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,$\frac{1}{2}$] | B. | [-$\frac{1}{4}$,$\frac{1}{2}$] | C. | [-$\frac{5}{3}$,+∞) | D. | (-∞,-$\frac{5}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com