
分析 (1)根据三角函数的定义求解即可.
(2)根据同角三角函数关系式求解.
解答 解:(1)角α的终边上一点P(m,-$\sqrt{3}$)(m≠0),且cosα=$\frac{{\sqrt{2}m}}{4}$
设知$x=m,y=-\sqrt{3}$,
∴${r^2}=|OP{|^2}={(-\sqrt{3})^2}+{m^2}$(O为原点),
则$r=\sqrt{3+{m^2}}$.
∴$cosα=\frac{m}{r}=\frac{{\sqrt{2}m}}{4}=\frac{m}{{2\sqrt{2}}}$,
∴$r=\sqrt{3+{m^2}}=2\sqrt{2}$,
即3+m2=8,
解得$m=±\sqrt{5}$.
(2)由(1)可知:当$m=\sqrt{5}$时,$cosα=\frac{{\sqrt{10}}}{4}$,$sinα=\frac{{-\sqrt{6}}}{4}$,$tanα=\frac{sinα}{cosα}=-\frac{{\sqrt{15}}}{5}$;
当$m=-\sqrt{5}$时,$cosα=-\frac{{\sqrt{10}}}{4}$,$sinα=\frac{{-\sqrt{6}}}{4}$,$tanα=\frac{sinα}{cosα}=\frac{{\sqrt{15}}}{5}$.
点评 本题考查任意角的三角函数的定义和同角三角函数的运用,基本知识的考查.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
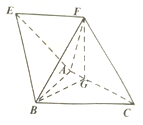 如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.
如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.
如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | ($\sqrt{2}$,2) | C. | (1,$\sqrt{2}$) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com