
| A. | $\frac{{\sqrt{3}}}{15}$ | B. | $\frac{{\sqrt{3}}}{16}$ | C. | $\frac{{\sqrt{2}}}{16}$ | D. | $\frac{{\sqrt{2}}}{14}$ |
分析 欲求直线OA被该封闭图形解得的线段长小于$\sqrt{2}$的概率,利用几何概型解决,只须利用定积分求出阴影图的面积,最后利用它们的面积比求得即可概率.
解答  解:抛物线y=x2与直线y=2所围成的面积为
解:抛物线y=x2与直线y=2所围成的面积为
S阴影=${∫}_{-\sqrt{2}}^{\sqrt{2}}$(2-x2)dx=(2x-$\frac{1}{3}$x3)|${\;}_{-\sqrt{2}}^{\sqrt{2}}$=$\frac{8\sqrt{2}}{3}$,
以O为原点,$\sqrt{2}$为半径的圆与抛物线y=x2分别交于B,C两点,
则OB=OC=$\sqrt{2}$,圆O的方程为x2+y2=2,
故A点只有在红色区域内时,
直线OA被直线OA被该封闭图形解得的线段长小于$\sqrt{2}$,
由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=2}\\{y={x}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$,
∴B(-1,1),C(1,1),
∴直线OB,OC的解析式分别为y=-x或y=x,
∴红色区域面积S红=${∫}_{-1}^{0}(-x-{x}^{2})dx$+${∫}_{0}^{1}$(x-x2)dx=(-$\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}$)|${\;}_{-1}^{0}$+($\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}$)|${\;}_{0}^{1}$=$\frac{1}{6}$+$\frac{1}{6}$,
∴直线OA被该封闭图形解得的线段长小于$\sqrt{2}$的概率P=$\frac{{S}_{红}}{{S}_{阴影}}$=$\frac{\frac{1}{3}}{\frac{8\sqrt{2}}{3}}$=$\frac{\sqrt{2}}{16}$,
故选:C
点评 本题考查了利用定积分求面积以及几何摡型知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
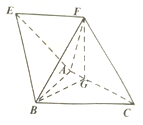 如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.
如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
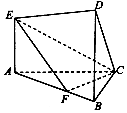 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com