
分析 通过a与$\frac{1}{2}$大小讨论,然后求解不等式的解集即可.
解答 解:当$a=\frac{1}{2}$时,不等式化为${(x-\frac{1}{2})^2}>0$解得:$x≠\frac{1}{2}$,
当$a>\frac{1}{2}$时,a>1-a原不等式解得:x<1-a或x>a,
当$a<\frac{1}{2}$时,a<1-a原不等式解得:x<a或x>1-a,
综上所述:当$a=\frac{1}{2}$时,不等式的解集为$\{x|x≠\frac{1}{2}\}$,
当$a>\frac{1}{2}$时,不等式的解集为{x|x<1-a或x>a},
当$a<\frac{1}{2}$时不等式的解集为{x|x<a或x>1-a}.
点评 本题考查含参数的二次不等式的解集的求法,考查转化思想以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
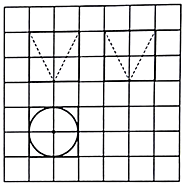 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )| A. | $20+\sqrt{5}π$ | B. | $24+\sqrt{5}π$ | C. | $20+(\sqrt{5}-1)π$ | D. | $24+(\sqrt{5}-1)π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({3,\frac{201}{10}})$ | B. | $({1,\frac{181}{10}})$ | C. | $({2\sqrt{2},+∞})$ | D. | $({2\sqrt{2}-2,+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{15}$ | B. | $\frac{{\sqrt{3}}}{16}$ | C. | $\frac{{\sqrt{2}}}{16}$ | D. | $\frac{{\sqrt{2}}}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
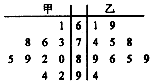 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com