
已知函数f(x)=x3-ax2-3x.
(1)若f(x)在[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)的单调区间.
(1)a≤0
(2)f(x)的单调递增区间为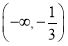 ,[3,+∞),f(x)的单调递减区间为
,[3,+∞),f(x)的单调递减区间为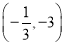 .
.
【解析】【解析】
(1)对f(x)求导,
得f′(x)=3x2-2ax-3.
由f′(x)≥0,得a≤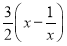 .
.
记t(x)=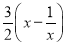 ,当x≥1时,t(x)是增函数,
,当x≥1时,t(x)是增函数,
∴t(x)min= (1-1)=0.∴a≤0.
(1-1)=0.∴a≤0.
(2)由题意,得f′(3)=0,
即27-6a-3=0,
∴a=4.∴f(x)=x3-4x2-3x,
f′(x)=3x2-8x-3.
令f′(x)=0,得x1=-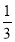 ,x2=3.
,x2=3.
当x变化时,f′(x)、f(x)的变化情况如下表:
x |
| - |
| 3 | (3,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ? | 极大值 | ? | 极小值 | ? |
∴f(x)的单调递增区间为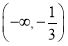 ,[3,+∞),f(x)的单调递减区间为
,[3,+∞),f(x)的单调递减区间为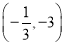 .
.


科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:解答题
已知f(x)是定义在集合M上的函数.若区间D⊆M,且对任意x0∈D,均有f(x0)∈D,则称函数f(x)在区间D上封闭.
(1)判断f(x)=x-1在区间[-2,1]上是否封闭,并说明理由;
(2)若函数g(x)=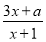 在区间[3,10]上封闭,求实数a的取值范围;
在区间[3,10]上封闭,求实数a的取值范围;
(3)若函数h(x)=x3-3x在区间[a,b](a,b∈Z,且a≠b)上封闭,求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:填空题
已知函数y=f(x)=x3+3ax2+3bx+c在x=2处有极值,其图像在x=1处的切线平行于直线6x+2y+5=0,则f(x)极大值与极小值之差为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练14 导数与函数单调性(解析版) 题型:解答题
已知函数f(x)=ln x,g(x)= x2-bx(b为常数).
x2-bx(b为常数).
(1)函数f(x)的图像在点(1,f(1))处的切线与g(x)的图像相切,求实数b的值;
(2)设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b的取值范围;
(3)若b>1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:解答题
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:填空题
曲线y=x3+ax+1的一条切线方程为y=2x+1,则实数a=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破四 高考立体几何(解析版) 题型:填空题
我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是________寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com