
【题目】改革开放四十年以来,北京市居民生活发生了翻天覆地的变化.随着经济快速增长、居民收入稳步提升,消费结构逐步优化升级,生活品质显著增强,美好生活蓝图正在快速构建.北京市城镇居民人均消费支出从1998年的7 500元增长到2017年的40 000元.1998年与2017年北京市城镇居民消费结构对比如下图所示:
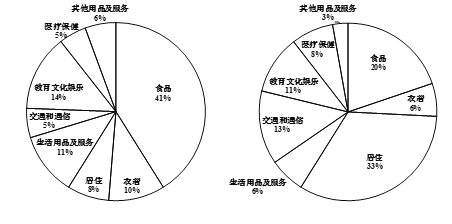
1998年北京市城镇居民消费结构 2017年北京市城镇居民消费结构
则下列叙述中不正确的是( )
A. 2017年北京市城镇居民食品支出占比同1998年相比大幅度降低
B. 2017年北京市城镇居民人均教育文化娱乐类支出同1998年相比有所减少
C. 2017年北京市城镇居民医疗保健支出占比同1998年相比提高约![]()
D. 2017年北京市城镇居民人均交通和通信类支出突破5 000元,大约是1998年的14倍
【答案】B
【解析】
2017年北京市城镇居民人均教育文化娱乐类支出:11%×40000=4400元,1998年北京市城镇居民人均教育文化娱乐类支出:14%×7500=1050元,故2017年北京市城镇居民人均教育文化娱乐类支出同1998年相比明显增加.
由1998年与2017年北京市城镇居民消费结构对比图,知:
在A中,2017年北京市城镇居民食品支出占比同1998年相比大幅度降低,故A正确;
在B中,2017年北京市城镇居民人均教育文化娱乐类支出:11%×40000=4400元,
1998年北京市城镇居民人均教育文化娱乐类支出:14%×7500=1050元,
故2017年北京市城镇居民人均教育文化娱乐类支出同1998年相比明显增加,故B错误;
在C中,2017年北京市城镇居民医疗保健支出占比同1998年相比提高约60%,故C正确;
在D中,2017年北京市城镇居民人均交通和通信类支出突破5000元,大约是1998年的14倍,故D正确.
故选:B.


科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 与
与![]() 均为菱形,
均为菱形,![]() ,且
,且![]() .
.
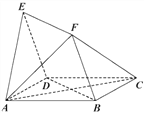
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若![]() 为线段
为线段![]() 上的一点,且满足直线
上的一点,且满足直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面推理过程中使用了类比推理方法,其中推理正确的是( )
A. 平面内的三条直线![]() ,若
,若![]() ,则
,则![]() .类比推出:空间中的三条直线
.类比推出:空间中的三条直线![]() ,若
,若![]() ,则
,则![]()
B. 平面内的三条直线![]() ,若
,若![]() ,则
,则![]() .类比推出:空间中的三条向量
.类比推出:空间中的三条向量![]() ,若
,若![]() ,则
,则![]()
C. 在平面内,若两个正三角形的边长的比为![]() ,则它们的面积比为
,则它们的面积比为![]() .类比推出:在空间中,若两个正四面体的棱长的比为
.类比推出:在空间中,若两个正四面体的棱长的比为![]() ,则它们的体积比为
,则它们的体积比为![]()
D. 若![]() ,则复数
,则复数![]() .类比推理:“若
.类比推理:“若![]() ,则
,则![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄冈市有很多名优土特产,黄冈市的蕲春县就有闻名于世的“蕲春四宝”![]() 蕲竹、蕲艾、蕲蛇、蕲龟
蕲竹、蕲艾、蕲蛇、蕲龟![]() ,很多人慕名而来旅游,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:
,很多人慕名而来旅游,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:
男 | 女 | 总计 | |
事先知道“蕲春四宝” | 8 |
|
|
事先不知道“蕲春四宝” |
| 4 | 36 |
总计 | 40 |
|
|
|
|
|
|
|
|
|
|
附:![]()
![]() 写出列联表中各字母代表的数字;
写出列联表中各字母代表的数字;
![]() 由以上列联表判断,能否在犯错误的概率不超过
由以上列联表判断,能否在犯错误的概率不超过![]() 的前提下认为购买“蕲春四宝”和是否“事先知道
的前提下认为购买“蕲春四宝”和是否“事先知道![]() 蕲春四宝
蕲春四宝![]() 有关系”?
有关系”?
![]() 从被询问的
从被询问的![]() 名事先知道“蕲春四宝”的顾客中随机选取2名顾客,求抽到的女顾客人数的分布列及其数学期望.
名事先知道“蕲春四宝”的顾客中随机选取2名顾客,求抽到的女顾客人数的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为节能环保,推进新能源汽车推广和应用,对购买纯电动汽车的用户进行财政补贴,财政补贴由地方财政补贴和国家财政补贴两部分组成. 某地补贴政策如下(![]() 表示纯电续航里程):
表示纯电续航里程):
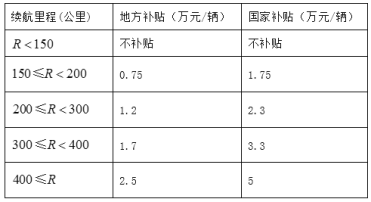
有![]() 三个纯电动汽车
三个纯电动汽车![]() 店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下:
店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下:
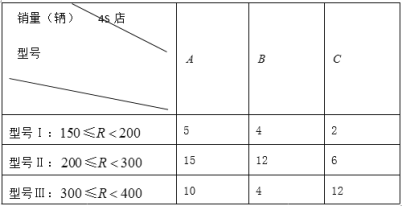
(每位客户只能购买一辆纯电动汽车)
(1)从上述购买纯电动汽车的客户中随机选一人,求此人购买的是![]() 店纯电动汽车且享受补贴不低于3.5万元的概率;
店纯电动汽车且享受补贴不低于3.5万元的概率;
(2)从上述![]() 两个纯电动汽车
两个纯电动汽车![]() 店的客户中各随机选一人,求恰有一人享受5万元财政补贴的概率;
店的客户中各随机选一人,求恰有一人享受5万元财政补贴的概率;
(3)从上述![]() 三个纯电动汽车
三个纯电动汽车![]() 店的客户中各随机选一人, 这3个人享受的财政补贴分别记为
店的客户中各随机选一人, 这3个人享受的财政补贴分别记为![]() . 求随机变量
. 求随机变量![]() 的分布列. 试比较数学期望
的分布列. 试比较数学期望![]() 的大小;比较方差
的大小;比较方差![]()
![]() 的大小. (只需写出结论)
的大小. (只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有学生15000人,其中男生10500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
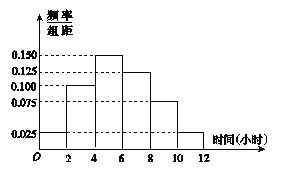
(2)根据这200个样本数据,得到学生每周平均体育运动时间的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .估计该校学生每周平均体育运动时间超过4小时的概率.
.估计该校学生每周平均体育运动时间超过4小时的概率.
(3)在样本数据中,有40位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.(把表简要画在答题卡上)
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
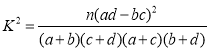
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】洛萨![]() 科拉茨
科拉茨![]() Collatz,
Collatz,![]() 是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半
是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半![]() 即
即![]() ;如果n是奇数,则将它乘3加
;如果n是奇数,则将它乘3加![]() 即
即![]() ,不断重复这样的运算,经过有限步后,一定可以得到
,不断重复这样的运算,经过有限步后,一定可以得到![]() 如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,
如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,![]() 对科拉茨
对科拉茨![]()
![]() 猜想,目前谁也不能证明,更不能否定
猜想,目前谁也不能证明,更不能否定![]() 现在请你研究:如果对正整数
现在请你研究:如果对正整数![]() 首项
首项![]() 按照上述规则施行变换
按照上述规则施行变换![]() 注:1可以多次出现
注:1可以多次出现![]() 后的第八项为1,则n的所有可能的取值为______.
后的第八项为1,则n的所有可能的取值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com