已知函数f(x)=x2-(a+2)x+alnx,其中a∈R.
(Ⅰ)若曲线y=f(x)在点(2,f(2))处的切线的斜率为1,求a的值;
(Ⅱ)求函数f(x)的单调区间.
解:(Ⅰ)由f(x)=x
2-(a+2)x+alnx,可知,函数定义域为{x|x>0},
且f′(x)=2x-(a+2)+

.由题意,f′(2)=4-(a+2)+

=1,
解得a=2.…(4分)
(Ⅱ)f′(x)=2x-(a+2)+

=
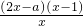
(x>0).
令f′(x)=0,得x
1=1,x
2=

.
(1)当a≤0时,

≤0,令f′(x)>0,得x>1;
令f′(x)<0,得0<x<1.
则函数f(x)的单调递减区间为(0,1),单调递增区间为(1,+∞).
(2)当0<

<2,即0<a<2时,令f′(x)>0,得0<x<

或x>1.
则函数f(x)的单调递增区间为(0,

),(1,+∞).
令f′(x)<0,得

<x<1.
则函数f(x)的单调递减区间为(

,1).
(3)当

=1,即a=2时,f′(x)≥0恒成立,则函数
f(x)的单调递增区间为(0,+∞).
(4)当

>1,即a>2时,令f′(x)>0,得0<x<1或x>

,
则函数f(x)的单调递增区间为(0,1),(

,+∞).
令f′(x)<0,得1<x<

.
则函数f(x)的单调递减区间为(1,

).…(13分)
分析:(Ⅰ)对函数f(x)求导,根据导数的几何意义可求f(x)的图象在点(2,f(2))处的切线斜率k,结合已知可求a
(II)先求函数f(x)的定义域为(0,+∞),要判断函数的单调区间,需要判断导数f′(x)的正负,分类讨论:分(1)当a≥0时,(2)当0<a<2时,(3)当a=2时,(4)当a>2时四种情况分别求解.
点评:本题主要考查了函数的导数的求解,利用导数判断函数的单调区间,体现了分类讨论思想的应用.

 .由题意,f′(2)=4-(a+2)+
.由题意,f′(2)=4-(a+2)+ =1,
=1, =
=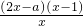 (x>0).
(x>0). .
. ≤0,令f′(x)>0,得x>1;
≤0,令f′(x)>0,得x>1; <2,即0<a<2时,令f′(x)>0,得0<x<
<2,即0<a<2时,令f′(x)>0,得0<x< 或x>1.
或x>1. ),(1,+∞).
),(1,+∞). <x<1.
<x<1. ,1).
,1). =1,即a=2时,f′(x)≥0恒成立,则函数
=1,即a=2时,f′(x)≥0恒成立,则函数 >1,即a>2时,令f′(x)>0,得0<x<1或x>
>1,即a>2时,令f′(x)>0,得0<x<1或x> ,
, ,+∞).
,+∞). .
. ).…(13分)
).…(13分)

 名校课堂系列答案
名校课堂系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<