
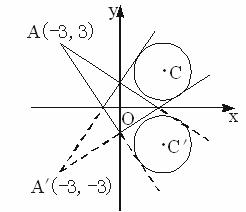
解:圆C:x2+y2-4x-4y+7=0的标准方程为(x-2)2+(y-2)2=1,
圆C关于x轴的对称圆C′的方程为(x-2)2+(y+2)2=1.
设光线l所在直线的方程为y-3=k(x+3).
依题意,它是圆C′的切线,从而点C′到直线l的距离为1,即![]() =1.
=1.
解得k=-![]() 或k=-
或k=-![]() .
.
∴光线l所在直线的方程为y-3=-![]() (x+3)或y-3=-
(x+3)或y-3=-![]() (x+3),即3x+4y-3=0或 4x+3y+3=0.
(x+3),即3x+4y-3=0或 4x+3y+3=0.
同理可求过点A′(-3,-3)的圆C的切线方程3x-4y-3=0或4x-3y+3=0为所求光线m所在直线的方程.
点评:本例复习了直线方程的点斜式、圆的切线方程的求法、点到直线的距离公式、配方法化圆的一般方程为标准方程及研究入射光线和反射光线问题时常用的找对称点或对称图形的方法.解题时需注意的问题是:直线的点斜式适用于斜率存在的情况.由图知此题中,入射光线所在直线应有两条,若k只有一解,应考虑k不存在的情况.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,则光线l所在直线方程为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com