Question

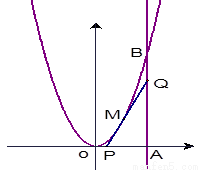
（本题满分10分）   如图，由y=0，x=8，y=x²围成的曲边三角形，在曲线弧OB上求一点M，使得过M所作的y=x²的切线PQ与OA，AB围成的三角形PQA面积最大。

                                                 

 

Answer 1

【答案】

（，）

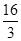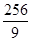【解析】

试题分析：如图，设点M（t，t²），容易求出过点M的切线的斜率为2t，即切线方程为y-t²=2t（x-t），（0≤t≤8）

当t=0时，切线为y=0，△PQA不存在，所以（0＜t≤8）．

在切线方程中令y=0，得到P点的横坐标为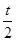，令x=8，得到Q点的纵坐标为16t-t²

所以S_△PQA= 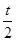（8-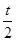）（16t-t²），

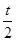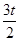令S′（t）=（8-）（8-）=0；

解可得得t=16（舍去）或t=；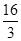

由二次函数的性质分析易得，

t=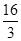是S_△PQA=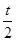（8-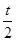）（16t-t²）的极大值点；

从而当t=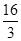时，面积S（t）有最大值S_max=S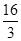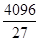（）=，此时M（，）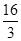

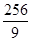考点：本题主要考查导数的几何意义的应用，应用导数求函数的最值问题。

点评：本题符合高考考试大纲，是一道颇具代表性的题目。