
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 的最小值为
的最小值为![]() ,且该椭圆的离心率为
,且该椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 上不同的两点,且
上不同的两点,且![]() ,若
,若![]() ,试问直线
,试问直线![]() 是否经过一个定点?若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
是否经过一个定点?若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
【答案】(1)![]() (2)直线
(2)直线![]() 过定点
过定点![]()
【解析】
(1)依题意得到方程组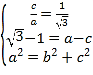 解得;
解得;
(2)已知![]() 且
且![]() ,可知点
,可知点![]() 同在
同在![]() 轴的上方或下方,
轴的上方或下方,
由对称性可知,若动直线![]() 经过一个定点,则该定点在
经过一个定点,则该定点在![]() 轴上,因为
轴上,因为![]() ,所以点
,所以点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,联立直线与椭圆方程,列出韦达定理,由直线
,联立直线与椭圆方程,列出韦达定理,由直线![]() 的斜率
的斜率![]() ,得直线
,得直线![]() 的方程为
的方程为![]() ,令
,令![]() ,计算其横坐标是否为定值.
,计算其横坐标是否为定值.
解:(1)依题意得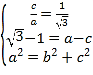 ,解得
,解得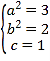 ,所以椭圆
,所以椭圆![]() ;
;
(2)直线![]() 过定点
过定点![]() ,
,
证明:已知![]() 且
且![]() ,可知点
,可知点![]() 同在
同在![]() 轴的上方或下方,
轴的上方或下方,
由对称性可知,若动直线![]() 经过一个定点,则该定点在
经过一个定点,则该定点在![]() 轴上,
轴上,
因为![]() ,所以点
,所以点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
联立 ,消去
,消去![]() 整理得
整理得![]() 又
又![]() ,
,
所以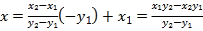 ,
,
由直线![]() 的斜率
的斜率![]() ,得直线
,得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得:
,得:![]() ,
,
由![]() ,
,
所以![]()
即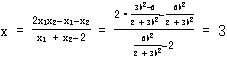 ,
,
所以直线![]() 过定点
过定点![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线![]() ,一光源在点
,一光源在点![]() 处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的点
处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的点![]() ,反射后,又射向抛物线上的点
,反射后,又射向抛物线上的点![]() ,再反射后又沿平行于抛物线的对称轴方向射出,途中遇到直线
,再反射后又沿平行于抛物线的对称轴方向射出,途中遇到直线![]() 上的
上的![]() 点,再反射后又射回点
点,再反射后又射回点![]() .设
.设![]() ,
,![]() 两点的坐标分别是
两点的坐标分别是![]() ,
,![]() .
.
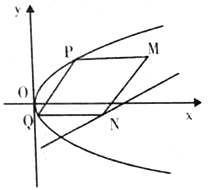
(1)证明:![]() ;
;
(2)若四边形![]() 是平行四边形,且点
是平行四边形,且点![]() 的坐标为
的坐标为![]() .求直线
.求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2019年的冬令营考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| 35 | 0.350 |
第3组 |
| 10 | 0.100 |
第4组 |
| 20 | 0.200 |
第5组 |
| 30 | 0.300 |
合计 | 100 | 1.00 | |
(1)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(2)在(1)的前提下,高校决定在这6名学生中,随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被A考官测试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设点![]() ,
,![]() ,
,![]() (其中
(其中![]() 表示a、b中的较大数)为
表示a、b中的较大数)为![]() 、
、![]() 两点的“切比雪夫距离”.
两点的“切比雪夫距离”.
(1)若![]() ,Q为直线
,Q为直线![]() 上动点,求P、Q两点“切比雪夫距离”的最小值;
上动点,求P、Q两点“切比雪夫距离”的最小值;
(2)定点![]() ,动点
,动点![]() 满足
满足![]()
![]() ,请求出P点所在的曲线所围成图形的面积.
,请求出P点所在的曲线所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知![]() ,且2an+1=an+1(n∈N*).
,且2an+1=an+1(n∈N*).
(1)求证:数列{an-1}是等比数列;
(2)若bn=nan,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图,长方体![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,过点
的中点,过点![]() 的平面
的平面![]() 与平面
与平面![]() 平行,且与长方体的面相交,交线围成一个几何图形.
平行,且与长方体的面相交,交线围成一个几何图形.
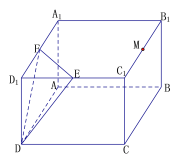
(1)在图中画出这个几何图形,并求这个几何图形的面积(画图说出作法,不用说明理由);
(2)求证:![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用![]() 局
局![]() 胜制(即先胜
胜制(即先胜![]() 局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以![]() 比
比![]() 获胜的概率;
获胜的概率;
(2)求乙获胜且比赛局数多于![]() 局的概率;
局的概率;
(3)求比赛局数![]() 的分布列,并求
的分布列,并求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com