
| ln[f′(x)+1]-lna-a2 |
| ln[f′(x)+1]-lna+2a2 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 3a |
| x2+2a |
| 3a |
| x2+2a |
| 3a |
| 4+2a |
| 3a |
| 4+2a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| x-a |
| x+2a |
| -x+a |
| x+2a |
| -3a |
| (x+2a)2 |
| x-a |
| x+2a |
| 3a |
| (x+2a)2 |
| -3a |
| (x1+2a)2 |
| 3a |
| (x2+2a)2 |
| 3a |
| x2+2a |
| 3a |
| x2+2a |
| 3a |
| 4+2a |
| 3a |
| 4+2a |
| 3a |
| 4+2a |
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| b |
| 4x+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在一项农业试验中,为了比较两种肥料对于某种果树的施肥效果,随机选取了施用这两种肥料的果树各10棵的产量(单位:kg):
在一项农业试验中,为了比较两种肥料对于某种果树的施肥效果,随机选取了施用这两种肥料的果树各10棵的产量(单位:kg):查看答案和解析>>
科目:高中数学 来源: 题型:
 某个公园有个池塘,其形状为直角三角形ABC,∠C=90°,AB=100米,BC=50米.
某个公园有个池塘,其形状为直角三角形ABC,∠C=90°,AB=100米,BC=50米.查看答案和解析>>
科目:高中数学 来源: 题型:
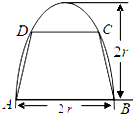 如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com