
 过抛物线
过抛物线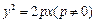 的焦点,并且与抛物线相交于
的焦点,并且与抛物线相交于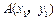 和
和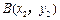 两点
两点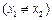 .求证:对于此抛物线的任意给定的一条弦
.求证:对于此抛物线的任意给定的一条弦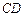 ,直线
,直线 不是
不是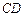 的垂直平分线.用反证法证明.
的垂直平分线.用反证法证明. 科目:高中数学 来源:不详 题型:单选题
| A.①② | B.①②④ | C.①②③ | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 为正整数,用数学归纳法证明
为正整数,用数学归纳法证明
 时,若已假设
时,若已假设 (
( 为偶数)真,则还需利用归纳假设再证( )
为偶数)真,则还需利用归纳假设再证( ) 时等式也成立 B
时等式也成立 B 、
、 时等式也成立
时等式也成立  时等式也成立 D、
时等式也成立 D、 时等式也成立
时等式也成立查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 都是偶数”,正确的反设为(***)
都是偶数”,正确的反设为(***)A. 都是奇数 都是奇数 | B. 中至多有一个是奇数 中至多有一个是奇数 |
C. 中至少有一个是奇数 中至少有一个是奇数 | D. 中恰有一个是奇数 中恰有一个是奇数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com