
 如图所示,已知圆O1与圆O2相交于A,B两点,过点A作圆O1的切线交圆O2于点C,过点B作两圆的割线,分别交圆O1,圆O2于点D,E,DE与AC相交于点P.
如图所示,已知圆O1与圆O2相交于A,B两点,过点A作圆O1的切线交圆O2于点C,过点B作两圆的割线,分别交圆O1,圆O2于点D,E,DE与AC相交于点P.分析 (1)连接AB,根据弦切角等于所夹弧所对的圆周角得到∠BAC=∠D,又根据同弧所对的圆周角相等得到∠BAC=∠E,等量代换得到∠D=∠E,根据内错角相等得到两直线平行即可;
(II)根据切割线定理得到AD2=DB•DE,利用AD是圆O2的切线,AD2=DB•DE,由此即可求DB的长.
解答 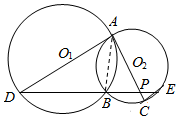 (1)证明:连接AB,
(1)证明:连接AB,
∵AC是圆O1的切线,∴∠BAC=∠D,
又∵∠BAC=∠E,∴∠D=∠E,∴AD∥EC
(2)解:设PB=x,PE=y,
∵PA=3,PC=1,∴xy=3①,
∵AD∥EC,∴$\frac{AP}{PC}=\frac{DP}{PE}=3$,且DP=3y
由AD是圆O2的切线,∴AD2=DB•DE,∴62=(3y-x)4y②
由①②可得,$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=2}\end{array}\right.$,∴BD=3y-x=$\frac{9}{2}$
点评 此题是一道综合题,要求学生灵活运用直线与圆相切和相交时的性质解决实际问题.本题的突破点是辅助线的连接.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{47}{6}$ | B. | $\frac{15}{2}$ | C. | $\frac{23}{3}$ | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com