
| A. | (-$\frac{9}{4}$,-2]∪(0,$\frac{1}{2}$] | B. | (-$\frac{11}{4}$,-2]∪(0,$\frac{1}{2}$] | C. | (-$\frac{9}{4}$,-2]∪(0,$\frac{2}{3}$] | D. | (-$\frac{11}{4}$,-2]∪(0,$\frac{2}{3}$] |
分析 由g(x)=f(x)-mx=0,即f(x)=mx,作出两个函数的图象,利用数形结合即可得到结论.
解答 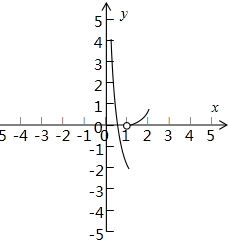 解:函数f(x)=$\left\{\begin{array}{l}{\frac{1}{x}-3,x∈(0,1]}\\{{2}^{x-1}-1,x∈(1,2]}\end{array}\right.$的图象如图所示.
解:函数f(x)=$\left\{\begin{array}{l}{\frac{1}{x}-3,x∈(0,1]}\\{{2}^{x-1}-1,x∈(1,2]}\end{array}\right.$的图象如图所示.
m∈(0,$\frac{1}{2}$]时,y=mx与图象两支有两个交点,
m<0时,由0<x≤1,$\frac{1}{x}$-3=mx,即mx2+3x-1=0,
方程有两解时,$\left\{\begin{array}{l}{9+4m>0}\\{0<-\frac{3}{2m}≤1}\\{m+2≤0}\end{array}\right.$,∴-$\frac{9}{4}$<m≤-2,
综上所述,(-$\frac{9}{4}$,-2]∪(0,$\frac{1}{2}$].
故选:A.
点评 本题主要考查函数零点的应用,利用数形结合是解决此类问题的基本方法.


科目:高中数学 来源: 题型:选择题
 如图,正方形ABCD的边长等于2,等腰三角形PAB中PA=PB,且平面PAB⊥平面ABCD,若直线PD与平面ABCD所成的角为$\frac{π}{4}$,则PA的长为( )
如图,正方形ABCD的边长等于2,等腰三角形PAB中PA=PB,且平面PAB⊥平面ABCD,若直线PD与平面ABCD所成的角为$\frac{π}{4}$,则PA的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
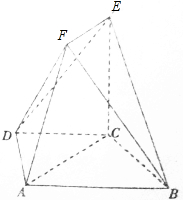 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=2,在梯形ACEF中,EF∥AC,且AC=2EF,CE=$\frac{\sqrt{6}}{4}$,且EC⊥平面ABCD.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=2,在梯形ACEF中,EF∥AC,且AC=2EF,CE=$\frac{\sqrt{6}}{4}$,且EC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{4}$,$\frac{1}{2}}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | [$\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com