[题目]已知x.y满足线性约束条件 .若z=x+4y的最大值与最小值之差为5.则实数λ的值为( )A.3B.C.D.1 题目和参考答案——青夏教育精英家教网—

【题目】已知x，y满足线性约束条件，若z=x+4y的最大值与最小值之差为5，则实数λ的值为（）
A.3
B.
C.
D.1

【答案】A
【解析】解：作出不等式组对应的平面区域，由得A（1，4），B（λ，λ﹣3）
由z=x+4y，得y=﹣ x+ ，
平移直线y=﹣ x+ ，由图象可知当直线经过点A时，直线y=﹣的截距最大，此时z最大．
z=1+4×4=17
当直线经过点B时，直线的截距最小，此时z最小．z=λ﹣3+4λ=5λ﹣3．
∵z=x+4y的最大值与最小值得差为5
∴17﹣（5λ﹣3）=20﹣5λ=5．
得λ=3．
故选：A．

作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最大值和最小值．建立方程关系进行求解即可．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知直线l：x+y+8=0，圆O：x2+y2=36（O为坐标原点），椭圆C： =1（a＞b＞0）的离心率为e= ，直线l被圆O截得的弦长与椭圆的长轴长相等．
（I）求椭圆C的方程；
（II）过点（3，0）作直线l，与椭圆C交于A，B两点设（O是坐标原点），是否存在这样的直线l，使四边形为ASB的对角线长相等？若存在，求出直线l的方程，若不存在，说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】甲、乙两人约定晚6点到晚7点之间在某处见面，并约定甲若早到应等乙半小时，而乙还有其他安排，若乙早到则不需等待，则甲、乙两人能见面的概率（）
A.
B.
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】数列{an}是公差为正数的等差数列，a2和 a5是方程x2﹣12x+27=0 的两实数根，数列{bn}满足3n﹣1bn=nan+1﹣（n﹣1）an ．
（Ⅰ）求an与bn；
（Ⅱ）设Tn为数列{bn}的前n项和，求Tn ，并求Tn＜7 时n的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在队内羽毛球选拔赛中，选手M与B1 ， B2 ， B3三位选手分别进行一场对抗赛，按以往多次比赛的统计，M获胜的概率分别为，且各场比赛互不影响．
（1）若M至少获胜两场的概率大于，则M入选下一轮，否则不予入选，问M是否会入选下一轮？
（2）求M获胜场数X的分布列和数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在学校组织的“环保知识”竞赛活动中，甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损，如图：
（Ⅰ）求乙班总分超过甲班的概率；
（Ⅱ）若甲班污损的学生成绩是90分，乙班污损的学生成绩为97分，现从甲乙两班所有选手成绩中各随机抽取2个，记抽取到成绩高于90分的选手的总人数为ξ，求ξ的分布列及数学成绩．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知O为坐标原点，F是双曲线的左焦点，A，B分别为Γ的左、右顶点，P为Γ上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E，直线 BM与y轴交于点N，若|OE|=2|ON|，则 Γ的离心率为（）
A.3
B.2
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆Γ： +y2=1（a＞1）的左焦点为F1 ，右顶点为A1 ，上顶点为B1 ，过F1 ， A1 ， B1三点的圆P的圆心坐标为（，）．
（Ⅰ）求椭圆的方程；
（Ⅱ）若直线l：y=kx+m（k，m为常数，k≠0）与椭圆Γ交于不同的两点M和N．
（i）当直线l过E（1，0），且 +2 = 时，求直线l的方程；
（ii）当坐标原点O到直线l的距离为时，求△MON面积的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若F1 ， F2是椭圆C： + =1（0＜m＜9）的两个焦点，椭圆上存在一点P，满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M．（Ⅰ）求椭圆C的方程；
（Ⅱ）过点（0，）的直线l与椭圆C交于两点A、B，线段AB的中垂线l1交x轴于点N，R是线段AN的中点，求直线l1与直线BR的交点E的轨迹方程．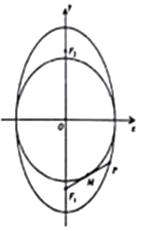

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学