
 研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得的数据如表:
研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得的数据如表:| 刹车时的车速(km/h) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| 刹车距离(m) | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |

|
|


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
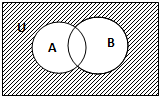
| A、[0,1] |
| B、[-1,2] |
| C、(-∞,-1)∪(2,+∞) |
| D、(-∞,-1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
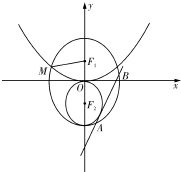 已知F1,F2是椭圆C1:
已知F1,F2是椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 3 |
| OA |
| OB |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 成都文化(分值) 人数 志愿者知识等级 |
10分 | 8分 | 6分 | 4分 |
| A | 5 | 1 | 7 | 0 |
| B | 3 | 2 | 7 | 1 |
| C | 1 | 0 | 6 | 3 |
| D | 1 | 1 | 2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 6 |
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.
如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.查看答案和解析>>
科目:高中数学 来源: 题型:
| x-2 |
| 2 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
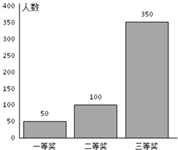 某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示.消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题.
某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示.消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com