
 如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.
如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.| ∫ | t 0 |
| 1 |
| 2 |
| 1 |
| 3 |
| | | t 0 |
| 1 |
| 6 |
| ∫ | 2 t |
| 1 |
| 3 |
| 1 |
| 2 |
| | | 2 t |
| 8 |
| 3 |
| 1 |
| 6 |
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 9 |
| 1 |
| 6 |
| 8 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 8 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |
8-4
| ||
| 3 |
| 2 |


科目:高中数学 来源: 题型:
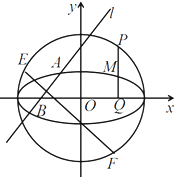 如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M.
如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M.| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| ln2 |
| 1 |
| ln3 |
| 1 |
| ln4 |
| 1 |
| lnn |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得的数据如表:
研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得的数据如表:| 刹车时的车速(km/h) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| 刹车距离(m) | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com