
分析 求导数f′(x),据题意便有f′(0)=a+b2-3=0,从而得出a=3-b2,从而ab=-b3+3b,并且根据a>0,b>0,可求出$0<b<\sqrt{3}$,并设g(b)=-b3+3b,求导数,根据导数符号便可判断出g(b)在b=1时取得最大值,这样即可求出ab的最大值.
解答 解:f′(x)=aex+b2-3;
∵f(x)在x=0处取得极值;
∴f′(0)=a+b2-3=0;
∴a=3-b2;
∴ab=(3-b2)b=-b3+3b;
∵a>0,b>0;
∴3-b2>0;
∴$0<b<\sqrt{3}$;
设g(b)=-b3+3b,g′(b)=-3b2+3=3(1-b2);
∴b∈(0,1)时,g′(b)>0,b$∈(1,\sqrt{3})$时,g′(b)<0;
∴b=1时,g(b)取最大值2;
即ab的最大值为2.
故答案为:2.
点评 考查函数极值的概念,以及根据导数符号判断函数极值和最值的方法及过程,清楚函数在极值点处的导数为0,注意正确求导.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:解答题
阅读下列有关光线的入射与反射的两个事实现象,现象(1):光线经平面镜反射满足入射角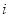 与反射角
与反射角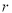 相等(如图1);现象(2):光线从椭圆的一个焦点出发经椭圆反射后通过另一个焦点(如图2).试结合上述事实现象完成下列问题:
相等(如图1);现象(2):光线从椭圆的一个焦点出发经椭圆反射后通过另一个焦点(如图2).试结合上述事实现象完成下列问题:
(1)有一椭圆型台球桌,长轴长为 ,短轴长为
,短轴长为 .将一放置于焦点处的桌球击出,经过球桌边缘的反射(假设球的反射完全符合现象(2)后第一次返回到该焦点时所经过的路程记为
.将一放置于焦点处的桌球击出,经过球桌边缘的反射(假设球的反射完全符合现象(2)后第一次返回到该焦点时所经过的路程记为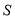 ,求
,求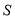 的值(用
的值(用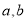 表示);
表示);
(2)结论:椭圆 上任一点
上任一点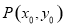 处的切线
处的切线 的方程为
的方程为 .记椭圆
.记椭圆 的方程为
的方程为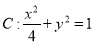 .
.
①过椭圆 的右准线上任一点
的右准线上任一点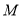 向椭圆
向椭圆 引切线,切点分别为
引切线,切点分别为 ,求证:直线
,求证:直线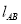 恒过一定点;
恒过一定点;
②设点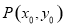 为椭圆
为椭圆 上位于第一象限内的动点,
上位于第一象限内的动点, 为椭圆
为椭圆 的左右焦点,点
的左右焦点,点 为
为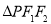 的内心,直线
的内心,直线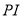 与
与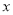 轴相交于点
轴相交于点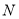 ,求点
,求点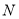 横坐标的取值范围.
横坐标的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
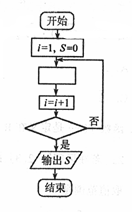
| A. | S=S+$\frac{i+1}{i}$,i≥100? | B. | S=S+$\frac{i+1}{i}$,i≥101? | C. | S=S+$\frac{i}{i-1}$,i≥100? | D. | S=S+$\frac{i}{i-1}$,i≥101? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (0,2) | C. | (-∞,2) | D. | (-∞,0)∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com