
分析 (Ⅰ)将m=-2代入f(x)的表达式,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)求出函数f(x)的导数,得到g(x)=-(x+1)+$\frac{1}{x+1}$,求出函数g(x)的导数,从而求出m的范围即可;
(Ⅲ)假设f(x)单调,求出f(x)的导数,结合二次函数的性质判断即可.
解答 解:(Ⅰ)当m=-2时,f(x)=(x2-2x)ex,
f′(x)=(x2-2)ex,
令f′(x)≥0,解得:x≥$\sqrt{2}$或x≤-$\sqrt{2}$,
∴f(x)在(-∞,-$\sqrt{2}$),($\sqrt{2}$,+∞)递增;
(Ⅱ)∵f′(x)=[x2+(m+2)x+m]ex,
由题意得f′(x)≤0对于x∈[1,3]恒成立,
∴x2+(m+2)x+m≤0,即m≤-$\frac{{x}^{2}+2x}{x+1}$=-(x+1)+$\frac{1}{x+1}$,
令g(x)=-(x+1)+$\frac{1}{x+1}$,则g′(x)=-1-$\frac{1}{{(x+1)}^{2}}$<0恒成立,
∴g(x)在区间[1,3]递减,g(x)min=g(3)=-$\frac{15}{4}$,
∴m的范围是(-∞,-$\frac{15}{4}$];
(Ⅲ)假设f(x)为R上的单调函数,
①若f(x)在R递增,则f′(x)≥0对x∈R恒成立,
即[x2+(m+2)x+m]ex≥0对x∈R恒成立,
∵ex>0,∴x2+(m+2)x+m≥0对x∈R恒成立,
而△=(m+2)2-4m=m2+4>0,
不满足x2+(m+2)x+m≥0对x∈R恒成立,
∴f(x)不是R上的单调递增函数;
②若f(x)在R递减,则f′(x)≤0对x∈R恒成立,
即[x2+(m+2)x+m]ex≤0对x∈R恒成立,
∵ex>0,∴x2+(m+2)x+m≤0对x∈R恒成立,
而函数h(x)=x2+(m+2)x+m的图象是开口向上的抛物线,
故x2+(m+2)x+m≤0不可能恒成立,
∴f(x)不是R上的单调递减函数,
综上,不存在实数m,使得f(x)为R上的单调函数.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及二次函数的性质,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:填空题
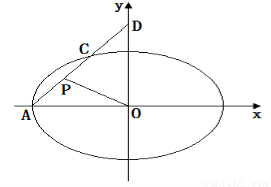
过椭圆 的左顶点
的左顶点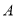 作斜率为
作斜率为 的直线
的直线 交椭圆于点
交椭圆于点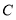 ,交
,交 轴于点
轴于点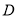 ,
, 为
为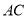 中点,定点
中点,定点 满足:对于任意的
满足:对于任意的 都有
都有 ,则
,则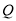 点的坐标为 .
点的坐标为 .
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
经市场调查,某门市部的一种小商品在过去的20天内的日销售量(件)与价格(元)均为时间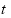 (天)的函数,且日销售量近似满足函数
(天)的函数,且日销售量近似满足函数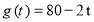 (件),而且销售价格近似满足于
(件),而且销售价格近似满足于 (元).
(元).
(1)试写出该种商品的日销售额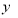 与时间
与时间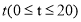 的函数表达式;
的函数表达式;
(2)求该种商品的日销售额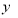 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 443 | B. | 328 | C. | 206 | D. | 864 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com