
分析 根据题设中的条件可设每天生产甲种产品x桶,乙种产品y桶,根据题设条件得出线性约束条件以及目标函数求出利润的最大值即可.
解答 解:设分别生产甲乙两种产品为x桶,y桶,利润为z元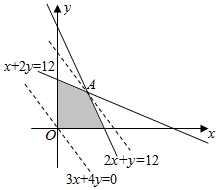
则根据题意可得$\left\{\begin{array}{l}{x+2y≤12}\\{2x+y≤12}\\{x,y≥0且x,y∈N}\end{array}\right.$,
目标函数z=300x+400y
作出不等式组表示的平面区域,如图所示
作直线L:3x+4y=0,然后把直线向可行域平移,
由图象知当直线经过A时,目标函数z=300x+400y的截距最大,此时z最大,
由$\left\{\begin{array}{l}{x+2y=12}\\{2x+y=12}\end{array}\right.$可得$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,即A(4,4),
此时z最大z=300×4+400×4=2800,
即该公司每天生产的甲4桶,乙4桶,可获得最大利润,最大利润为2800.
点评 本题考查用线性规划知识求利润的最大值,根据条件建立不等式关系,以及利用线性规划的知识进行求解是解决本题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
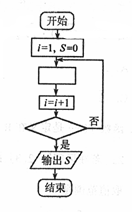
| A. | S=S+$\frac{i+1}{i}$,i≥100? | B. | S=S+$\frac{i+1}{i}$,i≥101? | C. | S=S+$\frac{i}{i-1}$,i≥100? | D. | S=S+$\frac{i}{i-1}$,i≥101? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com