
分析 (1)求出原函数的导函数,得到曲线f(x)在点(1,f(1))处的切线的斜率k=f′(1),再求出f(1),代入直线方程的点斜式求得曲线f(x)在点(1,f(1))处的切线;
(2)令g(x)=$\frac{1}{3}$x3+$\frac{1}{2}$x2+m,分别利用导数求出f(x),g(x)在定义域内的极大值与极小值,把方程f(x)-($\frac{1}{3}$x3+$\frac{1}{2}$x2+m)=0有3个不同的实数根,转化为两函数极值间的关系求解.
解答 解:(1)∵f(x)=(-x2+x-1)ex,
∴f′(x)=(-2x+1)ex+(-x2+x-1)ex =(-x2-x)ex,
∴曲线f(x)在点(1,f(1))处的切线的斜率k=f′(1)=-2e,
又∵f(1)=-e,
∴曲线f(x)在点(1,f(1))处的切线方程为y+e=-2e(x-1),
即2ex+y-e=0;
(2)∵f′(x)=(-x2-x)ex,
当x<-1或x>0时,f′(x)<0;当-1<x<0时,f′(x)>0.
∴f(x)在(-∞,-1),(0,+∞)内单调递减,在(-1,0)内单调递增.
∴f(x)在x=-1处取得极小值f(-1)=$-\frac{3}{e}$,在x=0处取得极大值f(0)=-1.
令g(x)=$\frac{1}{3}$x3+$\frac{1}{2}$x2+m,得g′(x)=x2+x,
当x<-1或x>0时,g′(x)>0;当-1<x<0时,g′(x)<0.
∴g(x)在(-∞,-1),(0,+∞)内单调递增,在(-1,0)内单调递减.
∴g(x)在x=-1处取得极大值g(-1)=$\frac{1}{6}+m$,在x=0处取得极小值g(0)=m.
∵方程f(x)-($\frac{1}{3}$x3+$\frac{1}{2}$x2+m)=0有3个不同的实数根,即函数f(x)与g(x)有3个不同交点.
∴$\left\{\begin{array}{l}{f(-1)<g(-1)}\\{f(0)>g(0)}\end{array}\right.$,即$\left\{\begin{array}{l}{-\frac{3}{e}<\frac{1}{6}+m}\\{-1>m}\end{array}\right.$,
∴$-\frac{3}{e}-\frac{1}{6}<m<-1$.
即实数m的取值范围是($-\frac{3}{e}-\frac{1}{6},-1$).
点评 不同考查利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的最值,考查数学转化思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
经市场调查,某门市部的一种小商品在过去的20天内的日销售量(件)与价格(元)均为时间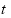 (天)的函数,且日销售量近似满足函数
(天)的函数,且日销售量近似满足函数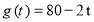 (件),而且销售价格近似满足于
(件),而且销售价格近似满足于 (元).
(元).
(1)试写出该种商品的日销售额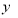 与时间
与时间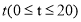 的函数表达式;
的函数表达式;
(2)求该种商品的日销售额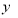 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com